题目内容
如图所示,在平行六面体ABCD—A1B1C1D1中,O是B1D1的中点,
求证:B1C∥平面ODC1.
求证:B1C∥平面ODC1.

证明略
设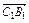 =a,
=a, =b,
=b,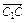 =c,
=c,
∵四边形B1BCC1为平行四边形,
∴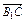 =c-a,
=c-a,
又O是B1D1的中点,
∴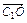 =
=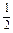 (a+b),
(a+b),
∴ =-
=-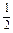 (a+b)
(a+b)
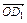 =
= -
-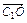 =b-
=b-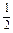 (a+b)=
(a+b)=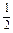 (b-a).
(b-a).
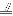 ∵D1D C1C,所以
∵D1D C1C,所以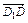 =c,
=c,
∴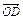 =
=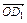 +
+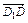 =
=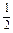 (b-a)+c.
(b-a)+c.
若存在实数x、y,使
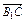 =x
=x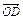 +y
+y (x,y∈R)成立,则
(x,y∈R)成立,则
c-a=x[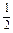 (b-a)+c]+y[-
(b-a)+c]+y[-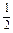 (a+b)]
(a+b)]
=-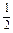 (x+y)a+
(x+y)a+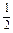 (x-y)b+xc.
(x-y)b+xc.
∵a、b、c不共线,
∴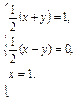 得
得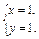
∴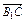 =
=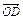 +
+ ,∴
,∴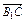 、
、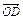 、
、 是共面向量,
是共面向量,
∵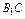 不在
不在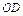 、
、 所确定的平面ODC1内,
所确定的平面ODC1内,
∴B1C∥平面ODC1.
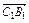 =a,
=a, =b,
=b,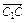 =c,
=c,∵四边形B1BCC1为平行四边形,
∴
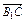 =c-a,
=c-a,又O是B1D1的中点,
∴
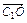 =
=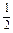 (a+b),
(a+b),∴
 =-
=-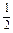 (a+b)
(a+b)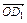 =
= -
-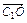 =b-
=b-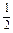 (a+b)=
(a+b)=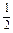 (b-a).
(b-a).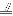 ∵D1D C1C,所以
∵D1D C1C,所以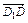 =c,
=c,∴
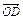 =
=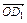 +
+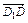 =
=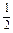 (b-a)+c.
(b-a)+c.若存在实数x、y,使
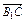 =x
=x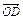 +y
+y (x,y∈R)成立,则
(x,y∈R)成立,则c-a=x[
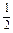 (b-a)+c]+y[-
(b-a)+c]+y[-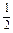 (a+b)]
(a+b)]=-
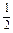 (x+y)a+
(x+y)a+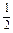 (x-y)b+xc.
(x-y)b+xc.∵a、b、c不共线,
∴
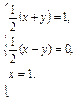 得
得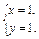
∴
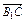 =
=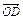 +
+ ,∴
,∴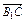 、
、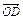 、
、 是共面向量,
是共面向量,∵
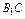 不在
不在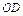 、
、 所确定的平面ODC1内,
所确定的平面ODC1内,∴B1C∥平面ODC1.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
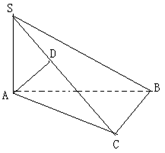
 是平行四边形
是平行四边形 平面外一点,
平面外一点, 分别是
分别是 上的点,且
上的点,且 =
= , 求证:
, 求证: 平面
平面

 平面
平面 ,
, 是圆O的直径,
是圆O的直径, 是圆O上的任一点,求证
是圆O上的任一点,求证 .
.
 是圆的直径,
是圆的直径, 垂直圆所在的平面,
垂直圆所在的平面, 是圆上任一点,
是圆上任一点, 平面
平面 .
.


 .
.
