题目内容
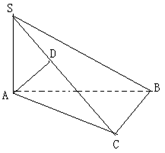
求证:AD⊥平面SBC
见解析
证明:SA⊥面ABC, BC⊥面ABC,ÞBC ⊥SA;
又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;
又ADÌ面SAC,∴ BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴ AD⊥面SBC。
又BC⊥AC,且AC、SA是面SAC内的两相交线,∴BC⊥面SAC;
又ADÌ面SAC,∴ BC⊥AD,
又已知SC⊥AD,且BC、SC是面SBC内两相交线,∴ AD⊥面SBC。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
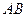
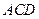
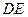
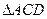
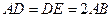 ,且
,且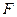 是
是 的中点.
的中点.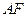 ∥平面
∥平面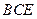 ;
; .
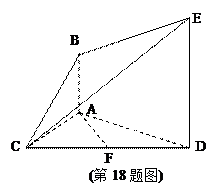
.
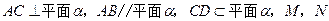 分别为
分别为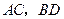 的中点,若
的中点,若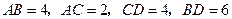 .
.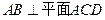 ;
;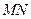 的长.
的长.
 中,求证:平面
中,求证:平面 平面
平面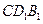 .
.