题目内容
正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.
证明略
方法一 如图所示,作PM∥AB交BE于M,作QN∥AB交BC于N,连接MN.

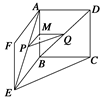
∵正方形ABCD和正方形ABEF有公共边AB,∴AE=BD.

又∵AP=DQ,∴PE=QB,
又∵PM∥AB∥QN,
 ∴
∴ ,
,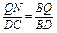 ,
, ,∴PM QN,
,∴PM QN,
∴四边形PMNQ为平行四边形,∴PQ∥MN.
又MN 平面BCE,PQ
平面BCE,PQ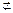 平面BCE,
平面BCE,
∴PQ∥平面BCE.
方法二 如图所示,连接AQ,并延长交BC于K,连接EK,
∵AE=BD,AP=DQ,
∴PE=BQ,
∴ =
= ①
①
又∵AD∥BK,∴ =
=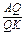 ②
②
由①②得 =
=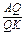 ,∴PQ∥EK.
,∴PQ∥EK.
又PQ 平面BCE,EK
平面BCE,EK 平面BCE,
平面BCE,
∴PQ∥平面BCE.
方法三 如图所示,在平面ABEF内,过点P作PM∥BE,交AB于点M,
连接QM.
∵PM∥BE,PM 平面BCE,
平面BCE,
即PM∥平面BCE,
∴ =
= ①
①
又∵AP=DQ,∴PE=BQ,
∴ =
= ②
②
由①②得 =
= ,∴MQ∥AD,
,∴MQ∥AD,
∴MQ∥BC,又∵MQ 平面BCE,∴MQ∥平面BCE.
平面BCE,∴MQ∥平面BCE.
又∵PM∩MQ=M,∴平面PMQ∥平面BCE,
PQ 平面PMQ,∴PQ∥平面BCE.
平面PMQ,∴PQ∥平面BCE.


∵正方形ABCD和正方形ABEF有公共边AB,∴AE=BD.

又∵AP=DQ,∴PE=QB,
又∵PM∥AB∥QN,
 ∴
∴ ,
,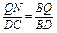 ,
, ,∴PM QN,
,∴PM QN,∴四边形PMNQ为平行四边形,∴PQ∥MN.
又MN
 平面BCE,PQ
平面BCE,PQ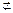 平面BCE,
平面BCE,∴PQ∥平面BCE.
方法二 如图所示,连接AQ,并延长交BC于K,连接EK,
∵AE=BD,AP=DQ,
∴PE=BQ,
∴
 =
= ①
①又∵AD∥BK,∴
 =
=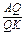 ②
②由①②得
 =
=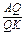 ,∴PQ∥EK.
,∴PQ∥EK.又PQ
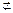 平面BCE,EK
平面BCE,EK 平面BCE,
平面BCE,∴PQ∥平面BCE.
方法三 如图所示,在平面ABEF内,过点P作PM∥BE,交AB于点M,
连接QM.
∵PM∥BE,PM
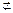 平面BCE,
平面BCE,即PM∥平面BCE,
∴
 =
= ①
①又∵AP=DQ,∴PE=BQ,
∴
 =
= ②
②由①②得
 =
= ,∴MQ∥AD,
,∴MQ∥AD,∴MQ∥BC,又∵MQ
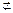 平面BCE,∴MQ∥平面BCE.
平面BCE,∴MQ∥平面BCE.又∵PM∩MQ=M,∴平面PMQ∥平面BCE,
PQ
 平面PMQ,∴PQ∥平面BCE.
平面PMQ,∴PQ∥平面BCE.
练习册系列答案
相关题目
 中,求证:平面
中,求证:平面 平面
平面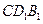 .
.
 的重心
的重心 ,作
,作 面
面 .
. 和△
和△ 都是直角三角形.
都是直角三角形.

 CC1.
CC1.
