题目内容
在正2006边形中,与所有边均不平行的对角线的条数为( )
| A.2006 | B. | C. | D. . . |
 C
C 正2n边形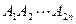 ,对角线共有
,对角线共有 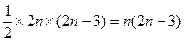 条。
条。
计算与一边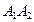 平行的对角线条数,因
平行的对角线条数,因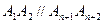 ,与
,与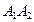 平行的对角线的端点只能取自2n-4个点,平行线共n-2条。故与某一边平行的对角线共n(n-2)条。由此可得与任何边都不平行的对角线共有n(2n-3)-n(n-2)=n(n-1)条。 因此正确选项是 C。
平行的对角线的端点只能取自2n-4个点,平行线共n-2条。故与某一边平行的对角线共n(n-2)条。由此可得与任何边都不平行的对角线共有n(2n-3)-n(n-2)=n(n-1)条。 因此正确选项是 C。
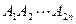 ,对角线共有
,对角线共有 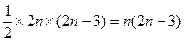 条。
条。计算与一边
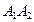 平行的对角线条数,因
平行的对角线条数,因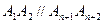 ,与
,与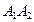 平行的对角线的端点只能取自2n-4个点,平行线共n-2条。故与某一边平行的对角线共n(n-2)条。由此可得与任何边都不平行的对角线共有n(2n-3)-n(n-2)=n(n-1)条。 因此正确选项是 C。
平行的对角线的端点只能取自2n-4个点,平行线共n-2条。故与某一边平行的对角线共n(n-2)条。由此可得与任何边都不平行的对角线共有n(2n-3)-n(n-2)=n(n-1)条。 因此正确选项是 C。
练习册系列答案
相关题目
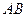
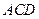
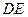
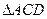
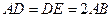 ,且
,且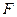 是
是 的中点.
的中点.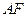 ∥平面
∥平面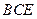 ;
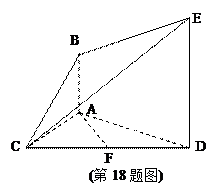
;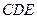 .
.
 在平面
在平面 内,过点
内,过点 和
和 ,应该怎样画线?
,应该怎样画线?
 的重心
的重心 ,作
,作 面
面 .
. 和△
和△ 都是直角三角形.
都是直角三角形.


 CC1.
CC1.