题目内容
【题目】谢宾斯基三角形是一种分形，由波兰数学家谢宾斯基在1915年提出，先作一个正三角形挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积，那么黑三角形为剩下的面积（我们称黑三角形为谢宾斯基三角形）．向图中第4个大正三角形中随机撒512粒大小均匀的细小颗粒物，则落在白色区域的细小颗粒物的数量约是（ ）
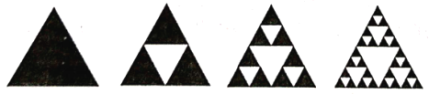
A.
B.
C.
D.
【答案】C
【解析】
设第一个三角形的面积为
，通过图形中的比例关系可确定黑色部分面积是首项为，公比为
的等比数列；通过计算第五个图形中黑色部分面积可确定白色部分面积；根据均匀随机数的思想可求得结果.
不妨设原三角形面积为，第一次挖去三角形的面积为
，剩余面积为，接下来每挖一次，对每个小完整三角形来说挖去的面积都是原完整三角形面积的，剩余面积为，故第二次挖去以后剩余面积为
，第三次挖去以后剩余面积为
，所以第
个图中白色区域的面积为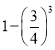
，所以落在白色区域的细小颗粒物约有
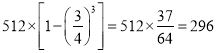（粒）．
故选：C
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
