题目内容
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
【答案】C
【解析】
由![]() 时解得
时解得![]() 值,求出
值,求出![]() ,即得
,即得![]() 与
与![]() 的表达式,从而计算
的表达式,从而计算![]() 的值.
的值.
令f(x)=g(x),即x22(a+2)x+a2=x2+2(a2)xa2+8,即x22ax+a24=0,解得x=a+2或x=a2.f(x)与g(x)的图象如图.
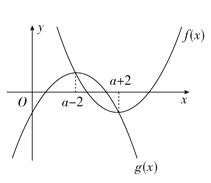
由图象及H1(x)的定义知H1(x)的最小值是f(a+2),H2(x)的最大值为g(a2),
∴AB=f(a+2)g(a2)=(a+2)22(a+2)2+a2+(a2)22(a2)2+a28=16.
故选:C.

练习册系列答案
相关题目