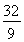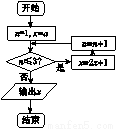题目内容
如图所示,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.

(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求二面角F-BC-A的余弦值.
(1)见解析(2)见解析(3)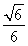
【解析】(1)证明:∵平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,∴AB∥DE.
又∵AB=DE,∴四边形ADEB为平行四边形,∴BE∥AD.
∵AD⊥平面DEFG,∴BE⊥平面DEFG.
(2)证明:设DG的中点为M,联结AM,MF,则DM= DG=2,
DG=2,

∵EF=2,EF∥DG,∴四边形DEFM是平行四边形,
∴MF=DE且MF∥DE,由(1)知,四边形ADEB为平行四边形,∴AB=DE且AB∥DE,∴AB=MF且AB∥MF,
∴四边形ABFM是平行四边形,
即BF∥AM,又BF?平面ACGD,AM?平面ACGD,故BF∥平面ACGD.

(3)由已知,AD,DE,DG两两垂直,建立如图所示的空间直角坐标系,则A(0,0,4),B(2,0,4),C(0,1,4),F(2,2,0),
故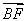 =(0,2,-4),
=(0,2,-4),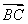 =(-2,1,0).
=(-2,1,0).
设平面FBC的法向量为n1=(x,y,z),则
令z=1,则n1=(1,2,1),
而平面ABC的法向量可为n2=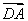 =(0,0,4),
=(0,0,4),
则cos〈n1,n2〉=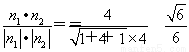 ,
,
由图形可知,二面角F-BC-A的余弦值为-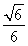

练习册系列答案
相关题目