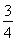题目内容
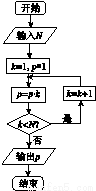
函数f(x)=sin(ωx+φ)ω>0,|φ|< 的部分图像如图Z3-4所示,将y=f(x)的图像向右平移
的部分图像如图Z3-4所示,将y=f(x)的图像向右平移 个单位长度后得到函数y=g(x)的图像.
个单位长度后得到函数y=g(x)的图像.

(1)求函数y=g(x)的解析式;
(2)在△ABC中,它的三个内角满足2sin2 =gC+
=gC+ +1,且其外接圆半径R=2,求△ABC的面积的最大值.
+1,且其外接圆半径R=2,求△ABC的面积的最大值.
(1)sin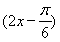 (2)
(2)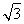
【解析】(1)由图知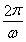 =4
=4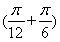 ,解得ω=2.
,解得ω=2.
∵f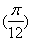 =sin
=sin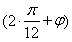 =1,∴
=1,∴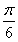 +φ=2kπ+
+φ=2kπ+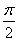 (k∈Z),即φ=2kπ+
(k∈Z),即φ=2kπ+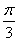 (k∈Z).
(k∈Z).
由-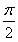 <φ<
<φ<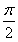 ,得φ=
,得φ=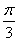 ,
,
∴f(x)=sin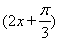 ,
,
∴f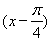 =sin
=sin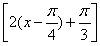 =sin
=sin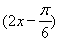 ,
,
即函数y=g(x)的解析式为g(x)=sin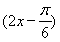 .
.
(2)∵2sin2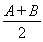 =g
=g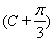 +1,
+1,
∴1-cos(A+B)=1+sin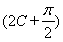 ,
,
∵cos(A+B)=-cos C,sin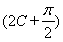 =cos 2C,
=cos 2C,
于是上式变为cos C=cos 2C,即cos C=2cos2C-1,整理得2cos2C-cos C-1=0,
解得cos C=-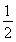 或1(舍),∴C=
或1(舍),∴C=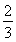 π.
π.
由正弦定理得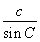 =2R=4,解得c=2
=2R=4,解得c=2 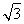 ,
,
于是由余弦定理得cos C=-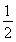 =
=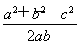 ,∴a2+b2=12-ab≥2ab,∴ab≤4(当且仅当a=b时等号成立),
,∴a2+b2=12-ab≥2ab,∴ab≤4(当且仅当a=b时等号成立),
∴S△ABC=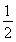 absin C=
absin C=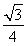 ab≤
ab≤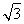 .
.
∴△ABC的面积的最大值为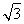 .
.

练习册系列答案
相关题目