题目内容
已知圆C1:x2+y2-2y=0,圆C2:x2+(y+1)2=4的圆心分别为C1,C2,P为一个动点,且直线PC1,PC2的斜率之积为- .
.
(1)求动点P的轨迹M的方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得|C1C|=|C1D|?若存在,求直线l的方程;若不存在,请说明理由.
(1) +y2=1(x≠0)(2)不存在
+y2=1(x≠0)(2)不存在
【解析】(1)两圆的圆心坐标分别为C1(0,1),和C2(0,-1),
设动点P的坐标为(x,y),则直线PC1,PC2的斜率分别为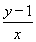 (x≠0)和
(x≠0)和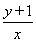 (x≠0).
(x≠0).
由已知条件得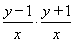 =-
=-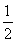 (x≠0),即
(x≠0),即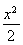 +y2=1(x≠0).
+y2=1(x≠0).
所以动点P的轨迹M的方程为 +y2=1(x≠0).
+y2=1(x≠0).
(2)假设存在满足条件的直线l,易知点A(2,0)在椭圆M的外部,当直线l的斜率不存在时,直线l与椭圆M无交点,此时不符合题意,所以直线l斜率存在,设为k,则直线l的方程为y=k(x-2).
联立方程组 得(2k2+1)x2-8k2x+8k2-2=0,①
得(2k2+1)x2-8k2x+8k2-2=0,①
依题意Δ=-8(2k2-1)>0,解得- <k<
<k<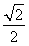 .
.
当-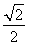 <k<
<k<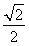 时,设交点分别为C(x1,y1),D(x2,y2),CD的中点为N(x0,y0),
时,设交点分别为C(x1,y1),D(x2,y2),CD的中点为N(x0,y0),
则x1+x2=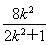 ,则x0=
,则x0=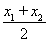 =
=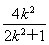 ,
,
所以y0=k(x0-2)=k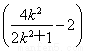 =
=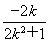 .
.
要使|C1C|=|C1D|,必须C1N⊥l,即k·kC1N=-1,
所以k· =-1,即k2-k+
=-1,即k2-k+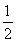 =0,
=0,
因为Δ1=1-4×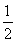 =-1<0,∴k2-k+
=-1<0,∴k2-k+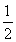 =0无解,
=0无解,
所以不存在直线,使得|C1C|=|C1D|,
综上所述,不存在直线l,使得|C1C|=|C1D|.

练习册系列答案
相关题目


