题目内容
(本小题满分12分)定义域为 的函数
的函数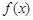 满足
满足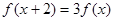 ,当
,当 ∈
∈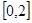 时,
时,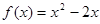
(1)当 ∈
∈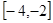 时,求
时,求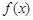 的解析式;
的解析式;
(2)当x∈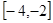 时,
时,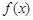 ≥
≥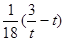 恒成立,求实数
恒成立,求实数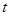 的取值范围.
的取值范围.
(1)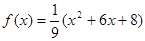 ;(2)
;(2)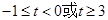
解析试题分析:(1)由已知条件可求出f(x+4)=9f(x),设x∈[-4,-2],则4+x∈[0,2],由已知可得f(x+4)的解析式,即可得解.(2)首先求出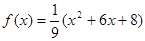 ,x∈
,x∈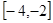 时的值域,由已知可得
时的值域,由已知可得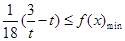 ,解不等式即可.
,解不等式即可.
试题解析:(1)由f(x+2)=3f(x),得f(x+4)=3f(x+2)=9f(x),
设x∈[-4,-2],则4+x∈[0,2],∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8,
因为f(x+4)=9f(x)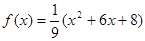 .
.
(2)因为x∈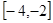 时,
时,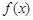 ≥
≥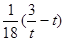 恒成立,所以x∈
恒成立,所以x∈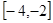 时,
时,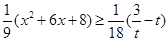 恒成立.而x∈
恒成立.而x∈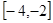 时,
时,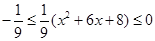 ,所以
,所以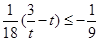 ,即
,即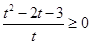 ,解得
,解得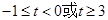
考点:1.分段函数;2.二次函数的性质;3.分式不等式的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
若每月用气量不超过最低额度
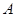
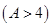 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费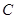
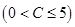 元;若用气量超过
元;若用气量超过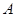 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付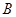 元.
元.⑴根据上面的表格求
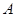 、
、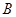 、
、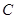 的值;
的值;⑵若用户第四月份用气30立方米,则应交煤气费多少元?
 .
.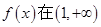 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;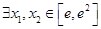 ,使
,使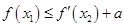 成立,求实数a的取值范围.
成立,求实数a的取值范围.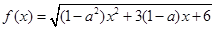 .若
.若 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围.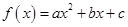 .
.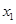 、
、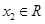 ,且
,且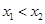 ,都有
,都有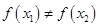 ,求证:关于
,求证:关于 的方程
的方程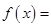
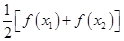 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于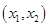 ;
;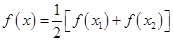 在
在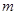 ,且
,且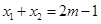 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为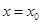 ,求证:
,求证: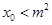 .
. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 上的最大值为12.
上的最大值为12. 上的最小值为
上的最小值为 ,求
,求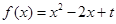 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.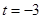 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;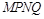 的面积的最大值。
的面积的最大值。 (单位:cm)满足关系:
(单位:cm)满足关系: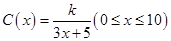 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设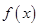 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.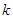 的值及
的值及