题目内容
已知函数 .
.
(1)若函数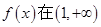 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(2)若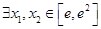 ,使
,使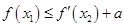 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(1)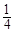 (2)
(2)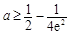 .
.
解析试题分析:(1) 根据原函数在区间上的单调递减转化为导数在该区间内小于等于零恒成立,再把恒成立转化为最值求解,在求解的过程中利用了二次三项式的配方;(2)命题的等价变换是解决本小题的关键,“若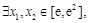 使
使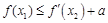 成立”等价于 “当
成立”等价于 “当 时,有
时,有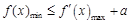 ”,于是整个问题就化为求函数的最值,然后利用导数分析单调性,进而求最值。
”,于是整个问题就化为求函数的最值,然后利用导数分析单调性,进而求最值。
试题解析:由已知函数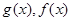 的定义域均为
的定义域均为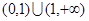 ,且
,且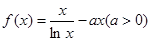 .
.
(1)函数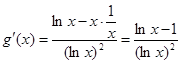 , 2分
, 2分
因f(x)在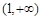 上为减函数,故
上为减函数,故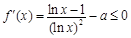 在
在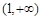 上恒成立.
上恒成立.
所以当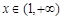 时,
时,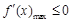 .
.
又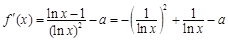
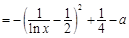 ,
,
故当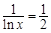 ,即
,即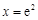 时,
时, .
.
所以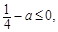 于是
于是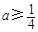 ,故a的最小值为
,故a的最小值为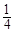 . 6分
. 6分
(2)命题“若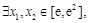 使
使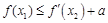 成立”等价于 “当
成立”等价于 “当 时,有
时,有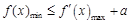 ”.
”.
由(Ⅱ),当 时,
时, ,
,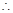
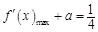 .
.
问题等价于:“当 时,有
时,有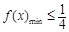 ”. 8分
”. 8分 当
当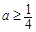 时,由(Ⅱ),
时,由(Ⅱ),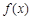 在
在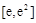 上为减函数,
上为减函数,
则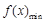 =
=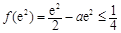 ,故
,故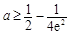 . 10分
. 10分 当
当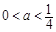 时,由于
时,由于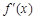
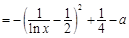 在
在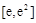 上为增函数,
上为增函数,
故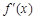 的值域为
的值域为 ,即
,即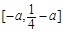 .
.
由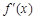 的单调性和值域知,
的单调性和值域知,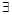 唯一
唯一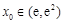 ,使
,使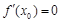 ,且满足:
,且满足:
当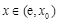 时,
时,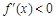 ,
,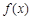 为减函数;
为减函数;
当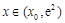 时,
时,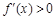 ,
,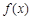 为增函数;
为增函数;
所以,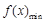 =
=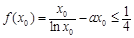 ,
,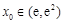 .
.
所以, ,与
,与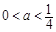 矛盾,不合题意. 11分
矛盾,不合题意. 11分
综上,得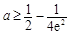 . 12分
. 12分
考点:1.导数公式;2.函数的单调性;3.恒成立问题;4.函数的最值以及命题的等价变换.

练习册系列答案
相关题目
 ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与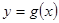 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围. ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记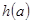 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
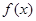 的值域;
的值域; 时,函数
时,函数 ,求
,求 的值和函数
的值和函数 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)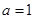 时,求
时,求 的单调区间;
的单调区间; 上无零点,求
上无零点,求 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求
 ;
; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的函数
的函数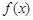 满足
满足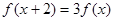 ,当
,当 ∈
∈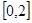 时,
时,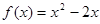
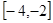 时,求
时,求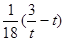 恒成立,求实数
恒成立,求实数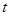 的取值范围.
的取值范围. 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出 万元,第二年需要支出
万元,第二年需要支出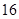 万元,第三年需要支出
万元,第三年需要支出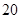 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出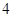 万元,而每年的生产收入都为
万元,而每年的生产收入都为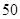 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用 年,
年,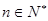 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这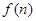 等于这
等于这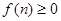 ,求
,求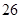 万元的价格出售该套设备;
万元的价格出售该套设备;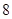 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.