题目内容
已知二次函数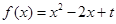 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当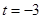 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形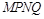 的面积的最大值。
的面积的最大值。
(1)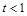 且
且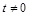 ;(2)圆F的方程为
;(2)圆F的方程为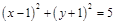 ;(3)四边形
;(3)四边形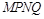 的面积的最大值为
的面积的最大值为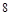 .
.
解析试题分析:(1)利用一元二次方程根的判别式易求得结果;(2)当 时,
时,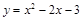 ,分别令
,分别令 得二次函数与两坐标轴的三个不同交点坐标,再设圆的一般方程或标准方程利用待定系数法求得圆的方程;(3)画出图形,利用垂径定理和勾股定理表示
得二次函数与两坐标轴的三个不同交点坐标,再设圆的一般方程或标准方程利用待定系数法求得圆的方程;(3)画出图形,利用垂径定理和勾股定理表示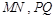 ,列出面积函数,利用均值不等式求四边形
,列出面积函数,利用均值不等式求四边形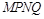 的面积的最大值.
的面积的最大值.
试题解析:(1)由已知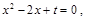 由
由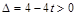 及
及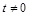 ,得
,得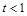 且
且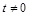 . 4分
. 4分
(2)当 时,
时,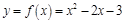 ,分别令
,分别令 得二次函数与两坐标轴的三个不同交点坐标
得二次函数与两坐标轴的三个不同交点坐标 设圆F的方程为
设圆F的方程为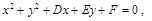 则
则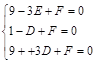 ,解得
,解得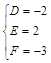 ,所以圆
,所以圆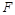 的方程为
的方程为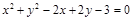 ,即
,即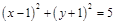 . 8分
. 8分
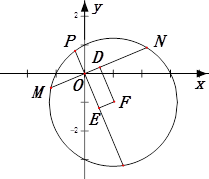
(3)如图: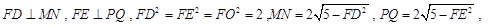
 四边形
四边形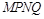 的面积
的面积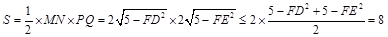 .
.
 四边形
四边形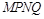 的面积的最大值为
的面积的最大值为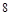 . 14分
. 14分
考点:1、直线与抛物线位置关系;2、圆的方程的求法;3、解析几何最值问题.

练习册系列答案
相关题目
 ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记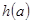 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围. 的函数
的函数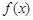 满足
满足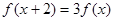 ,当
,当 ∈
∈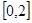 时,
时,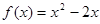
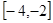 时,求
时,求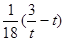 恒成立,求实数
恒成立,求实数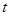 的取值范围.
的取值范围.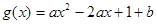 (
(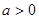 )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在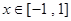 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.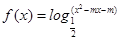 .
. )上是增函数,求实数m的取值范围.
)上是增函数,求实数m的取值范围.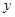 万元与投入
万元与投入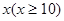 万元之间满足:
万元之间满足: 为常数。当
为常数。当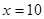 万元时,
万元时,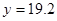 万元;
万元;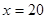 万元时,
万元时,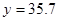 万元。 (参考数据:
万元。 (参考数据: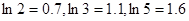 )
) 的解析式;
的解析式; 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。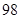 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出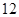 万元,第二年需要支出
万元,第二年需要支出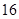 万元,第三年需要支出
万元,第三年需要支出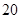 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出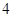 万元,而每年的生产收入都为
万元,而每年的生产收入都为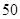 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用 年,
年,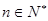 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这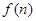 等于这
等于这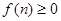 ,求
,求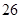 万元的价格出售该套设备;
万元的价格出售该套设备;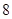 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由. ,其中
,其中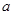 为大于零的常数,
为大于零的常数,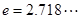 ,函数
,函数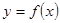 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为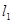 ,函数
,函数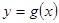 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为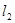 ,且
,且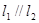 .
.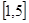 上存在
上存在 使不等式
使不等式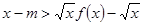 成立,求实数
成立,求实数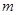 的取值范围;
的取值范围;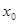 ,我们把
,我们把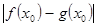 的值称为两函数在
的值称为两函数在 千件,需另投入成本为
千件,需另投入成本为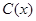 ,当年产量不足80千件时,
,当年产量不足80千件时,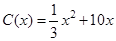 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,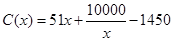 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.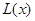 (万元)关于年产量
(万元)关于年产量