题目内容
函数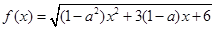 .若
.若 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围.
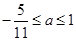 .
.
解析试题分析:由 的定义域为
的定义域为 可知
可知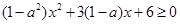 恒成立,这时要分
恒成立,这时要分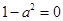 和
和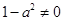 两种情况讨论,当
两种情况讨论,当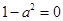 时,比较简单,易得结果,当
时,比较简单,易得结果,当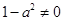 时,函数
时,函数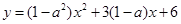 为二次函数,要使
为二次函数,要使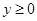 恒成立,由二次函数的图象应有,
恒成立,由二次函数的图象应有,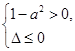 ,如此便可求出
,如此便可求出 的取值范围.
的取值范围.
试题解析:(1)当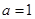 时,
时,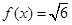 ,
, 的定义域为
的定义域为 ,符合题意;
,符合题意;
(2)当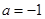 时,
时,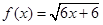 ,
, 的定义域不为
的定义域不为 ,所以
,所以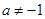 ;
;
(3)当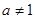
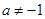 时,
时, 的定义域为
的定义域为 知抛物线
知抛物线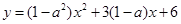 全部在
全部在 轴上方(或在上方相切),此时应有
轴上方(或在上方相切),此时应有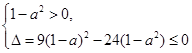 ,解得
,解得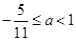 ;
;
综合(1),(2),(3)有 的取值范围是
的取值范围是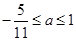 .
.
考点:二次函数、函数的定义域.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 ;
;

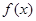 的值域;
的值域; 时,函数
时,函数 ,求
,求 的值和函数
的值和函数
 ;
; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.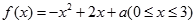 的最大值为
的最大值为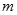 ,最小值为
,最小值为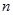 ,其中
,其中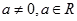 .
.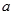 表示);
表示);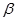 的顶点与平面直角坐标系
的顶点与平面直角坐标系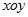 中的原点
中的原点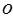 重合,始边与
重合,始边与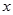 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点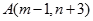 .求
.求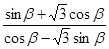 的值.
的值. 的函数
的函数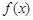 满足
满足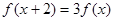 ,当
,当 ∈
∈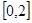 时,
时,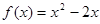
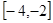 时,求
时,求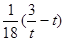 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 且
且 ,函数
,函数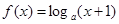 ,
,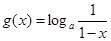 ,记
,记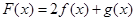 .
.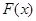 的定义域
的定义域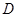 的表达式及其零点;
的表达式及其零点;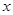 的方程
的方程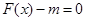 在区间
在区间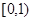 内仅有一解,求实数
内仅有一解,求实数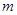 的取值范围.
的取值范围.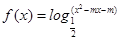 .
. )上是增函数,求实数m的取值范围.
)上是增函数,求实数m的取值范围.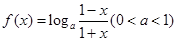 .
. 的定义域
的定义域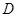 ,并判断
,并判断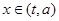 时,函数
时,函数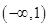 ,求
,求 与
与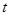 的值.
的值.