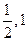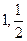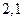题目内容
(本小题满分14分)设函数f (x)满足f (0) =1,且对任意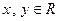 ,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
(Ⅲ)求数列{an}的前n项和Sn.
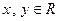 ,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;(Ⅲ)求数列{an}的前n项和Sn.
(Ⅰ)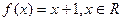 (Ⅱ) an = 2×3n-1-1(Ⅲ)3n-n-2
(Ⅱ) an = 2×3n-1-1(Ⅲ)3n-n-2
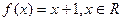 (Ⅱ) an = 2×3n-1-1(Ⅲ)3n-n-2
(Ⅱ) an = 2×3n-1-1(Ⅲ)3n-n-2(I) ∵f (0) =1.
令x=y=0得f (1) = f (0) f (0)-f (0)-0+2="2 "
再令y=0得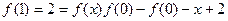 ,
,
所以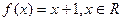 5分
5分
(II) ∵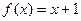 ,∴an+1=3f (an)-1= 3an+2,
,∴an+1=3f (an)-1= 3an+2,
∴an+1+1=3(an+1),
又a1+1=2,∴数列{an+1} 是公比为3的等比数列
∴an +1= 2×3n-1,即an = 2×3n-1-1 10分
(III) Sn = a1 + a2 + … + an
=2×(30+31+32+ ×××××× + 3n-1)-n
=3n-n-2 14分
令x=y=0得f (1) = f (0) f (0)-f (0)-0+2="2 "
再令y=0得
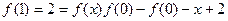 ,
, 所以
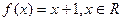 5分
5分(II) ∵
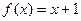 ,∴an+1=3f (an)-1= 3an+2,
,∴an+1=3f (an)-1= 3an+2, ∴an+1+1=3(an+1),
又a1+1=2,∴数列{an+1} 是公比为3的等比数列
∴an +1= 2×3n-1,即an = 2×3n-1-1 10分
(III) Sn = a1 + a2 + … + an
=2×(30+31+32+ ×××××× + 3n-1)-n
=3n-n-2 14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
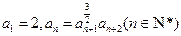 .
.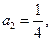 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);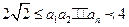 对n≥2恒成立,求a2的值。
对n≥2恒成立,求a2的值。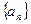 满足
满足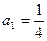 ,
,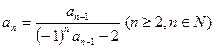 .
.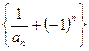 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;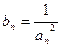 ,求数列
,求数列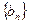 的前
的前 项和
项和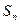 ;(3)设
;(3)设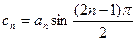 ,数列
,数列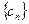 的前
的前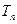 .求证:对任意的
.求证:对任意的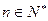 ,
,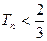 .
.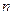 为正整数时,区间
为正整数时,区间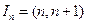 ,
,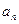 表示函数
表示函数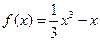 在
在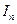 上函数值取整数值的个数,当
上函数值取整数值的个数,当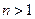 时,记
时,记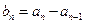 .当
.当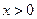 ,
,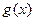 表示把
表示把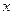 “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如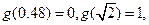
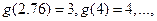 当
当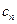 表示满足
表示满足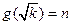 的正整数
的正整数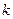 的个数.
的个数.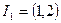 的单调性;
的单调性;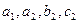 ;
;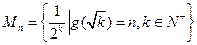 中所有元素之和为
中所有元素之和为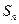 ,记
,记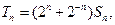 求证:
求证: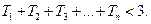
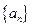 满足递推关系
满足递推关系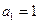 且
且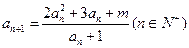 .
.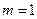 时,求数列
时,求数列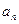 ;(2) 当
;(2) 当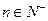 时,数列
时,数列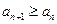 恒成立,求
恒成立,求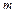 的取值范围;(3) 在
的取值范围;(3) 在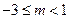 时,证明:
时,证明: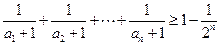 .
.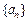 中,公差d > 0,其前n项和为
中,公差d > 0,其前n项和为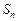 ,且满足
,且满足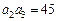 ,
,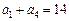 ,
,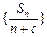 为等差数列.
为等差数列.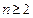 时,其前n项和满足
时,其前n项和满足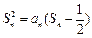
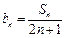 ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.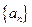 的前
的前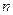 项和为
项和为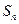 ,若
,若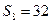 ,
,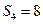 ,则它的首项与公差分别是( )
,则它的首项与公差分别是( )