题目内容
(本小题满分12分,(Ⅰ)小问6分.(Ⅱ)小问6分)
设各项均为正数的数列{an}满足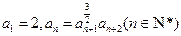 .
.
(Ⅰ)若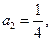 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);
(Ⅱ)若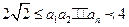 对n≥2恒成立,求a2的值。
对n≥2恒成立,求a2的值。
设各项均为正数的数列{an}满足
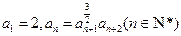 .
.(Ⅰ)若
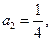 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);(Ⅱ)若
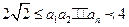 对n≥2恒成立,求a2的值。
对n≥2恒成立,求a2的值。(Ⅰ)见解析。
(Ⅱ)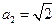
(Ⅱ)
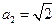
本题主要考查数列、等比数列以及不等式等基本知识,考查学生的探索、化归的数学思想与推理能力。
(I)因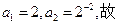
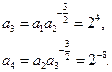
由此有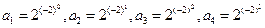 ,故猜想
,故猜想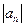 的通项为
的通项为
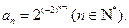
从而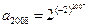
(Ⅱ)令xn=log2an.则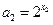 ,故只需求x2的值。
,故只需求x2的值。
设Sn表示xn的前n项和,则a1a2…an=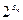 ,由2
,由2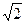 ≤a1a2…an<4得
≤a1a2…an<4得
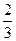 ≤Sn=x1+x2+…+xn<2 (n≥2).
≤Sn=x1+x2+…+xn<2 (n≥2).
因上式对n=2成立,可得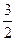 ≤x1+x2,又由a1=2,得x1=1,故x2≥
≤x1+x2,又由a1=2,得x1=1,故x2≥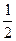 .
.
由于a1=2,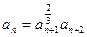 (n∈N*),得
(n∈N*),得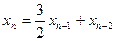 (n∈N*),即
(n∈N*),即
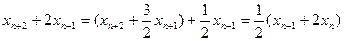 ,
,
因此数列{xn+1+2xn}是首项为x2+2,公比为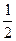 的等比数列,故
的等比数列,故
xn+1+2xn=(x2+2)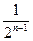 (n∈N*).
(n∈N*).
将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+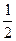 +…+
+…+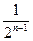 )=(x2+2)(2-
)=(x2+2)(2-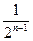 )(n≥2).
)(n≥2).
因Sn<2,Sn+1<2(n≥2)且x1=1,故
(x2+2)(2-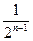 )<5(n≥2).
)<5(n≥2).
因此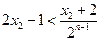 (n≥2).
(n≥2).
下证x2≤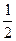 ,若不然,假设x2>
,若不然,假设x2>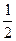 ,则由上式知,不等式
,则由上式知,不等式
2n-1<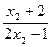
对n≥2恒成立,但这是不可能的,因此x2≤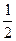 .
.
又x2≥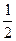 ,故x2=
,故x2=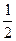 ,所以
,所以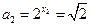
(I)因
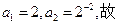
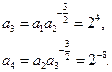
由此有
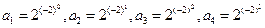 ,故猜想
,故猜想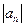 的通项为
的通项为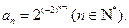
从而
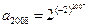
(Ⅱ)令xn=log2an.则
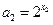 ,故只需求x2的值。
,故只需求x2的值。设Sn表示xn的前n项和,则a1a2…an=
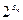 ,由2
,由2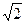 ≤a1a2…an<4得
≤a1a2…an<4得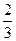 ≤Sn=x1+x2+…+xn<2 (n≥2).
≤Sn=x1+x2+…+xn<2 (n≥2).因上式对n=2成立,可得
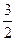 ≤x1+x2,又由a1=2,得x1=1,故x2≥
≤x1+x2,又由a1=2,得x1=1,故x2≥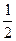 .
.由于a1=2,
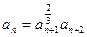 (n∈N*),得
(n∈N*),得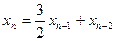 (n∈N*),即
(n∈N*),即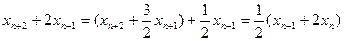 ,
,因此数列{xn+1+2xn}是首项为x2+2,公比为
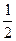 的等比数列,故
的等比数列,故xn+1+2xn=(x2+2)
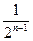 (n∈N*).
(n∈N*).将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+
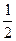 +…+
+…+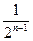 )=(x2+2)(2-
)=(x2+2)(2-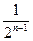 )(n≥2).
)(n≥2).因Sn<2,Sn+1<2(n≥2)且x1=1,故
(x2+2)(2-
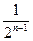 )<5(n≥2).
)<5(n≥2).因此
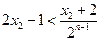 (n≥2).
(n≥2).下证x2≤
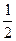 ,若不然,假设x2>
,若不然,假设x2>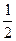 ,则由上式知,不等式
,则由上式知,不等式2n-1<
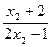
对n≥2恒成立,但这是不可能的,因此x2≤
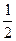 .
.又x2≥
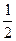 ,故x2=
,故x2=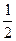 ,所以
,所以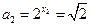

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
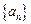 中,
中,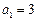 ,
,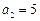 ,其前
,其前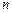 项和
项和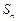 满足
满足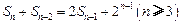 .令
.令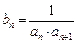 .
.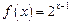 ,求证:
,求证: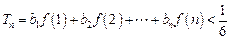 (
(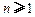 ).
).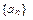 满足
满足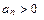 ,且对一切
,且对一切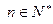 有
有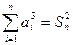 ,其中
,其中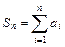 ,
, 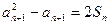 ,并求数列
,并求数列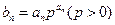 ,求数列
,求数列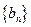 的前
的前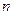 项和
项和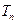 ;
;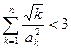 .
. 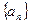 及等差数列
及等差数列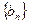 ,其中
,其中 ,公差
,公差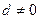 ,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和
,将这两个数列对应项相加得到一个新的数列1,1,2,…,求这个新数列的前10项之和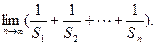
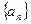 的公比为
的公比为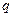 ,前n项和为
,前n项和为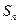 ,若
,若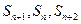 成等差数列,则
成等差数列,则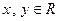 ,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I) 求f (x) 的解析式;(II) 若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;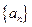 满足
满足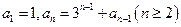 ,试写出
,试写出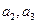 , 并求数列
, 并求数列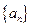 中,
中,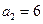 ,
,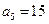 ,若
,若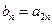 ,则数列
,则数列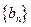 的前5项和等于( )
的前5项和等于( )