题目内容
已知函数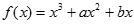 在
在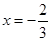 与
与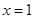 处都取得极值。
处都取得极值。
(1)求函数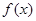 的解析式;(2)求函数
的解析式;(2)求函数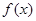 在区间[-2,2]的最大值与最小值
在区间[-2,2]的最大值与最小值
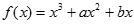 在
在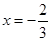 与
与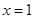 处都取得极值。
处都取得极值。(1)求函数
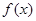 的解析式;(2)求函数
的解析式;(2)求函数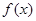 在区间[-2,2]的最大值与最小值
在区间[-2,2]的最大值与最小值
(1) (2)
(2)
 (2)
(2)
本试题主要考查了导数在研究函数中的运用。
解:(1)f(x)=x3+ax2+bx,f¢(x)=3x2+2ax+b ………………1分
由f¢( )=
)= ,f¢(1)=3+2a+b=0 ………………3分
,f¢(1)=3+2a+b=0 ………………3分
得a= ,b=-2 经检验,a=
,b=-2 经检验,a= ,b=-2符合题意
,b=-2符合题意
 ………………6分
………………6分
(2)由(1)得f¢(x)=3x2-x-2=(3x+2)(x-1), ………………7分
列表如下:
……9分

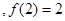 ………11分
………11分

解:(1)f(x)=x3+ax2+bx,f¢(x)=3x2+2ax+b ………………1分
由f¢(
 )=
)= ,f¢(1)=3+2a+b=0 ………………3分
,f¢(1)=3+2a+b=0 ………………3分得a=
 ,b=-2 经检验,a=
,b=-2 经检验,a= ,b=-2符合题意
,b=-2符合题意 ………………6分
………………6分 (2)由(1)得f¢(x)=3x2-x-2=(3x+2)(x-1), ………………7分
列表如下:
| x | (-2,- ) ) | - | (- ,1) ,1) | 1 | (1,2) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |

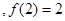 ………11分
………11分 

练习册系列答案
相关题目
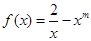 ,且
,且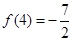 .
.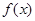 在
在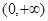 上的单调性,并给予证明;
上的单调性,并给予证明; 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点 处的切线垂直于直线
处的切线垂直于直线 .
. 的值;
的值; ,若方程
,若方程 有三个不相等的实根,求
有三个不相等的实根,求 的取值范围.
的取值范围. (单位:万元)与日产量x(单位:吨)满足函数关系式
(单位:万元)与日产量x(单位:吨)满足函数关系式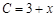 ,每日的销售额S(单位:万元)与日产量x的函数关系式
,每日的销售额S(单位:万元)与日产量x的函数关系式
 ,且当
,且当 时,
时, .(1)求
.(1)求 的值;(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值。
的值;(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值。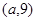 在函数
在函数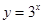 的图象上,则
的图象上,则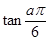 的值为
的值为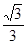
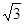
 对
对 且
且 恒有
恒有 ,则使
,则使 成立的实数
成立的实数 的取值范围是___▲___.
的取值范围是___▲___. .
.