题目内容
已知函数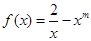 ,且
,且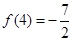 .
.
(1) 求m的值;
(2) 判断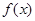 在
在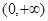 上的单调性,并给予证明;
上的单调性,并给予证明;
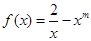 ,且
,且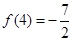 .
.(1) 求m的值;
(2) 判断
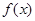 在
在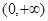 上的单调性,并给予证明;
上的单调性,并给予证明;(1)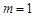 ;(2)见解析.
;(2)见解析.
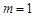 ;(2)见解析.
;(2)见解析.本试题主要考查了函数的性质的运用。
解:(1)由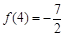 得:
得: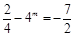 ,即:
,即: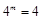 ,解得:
,解得: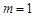 ;…………4分
;…………4分
(2) 函数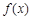 在
在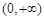 上为减函数。…………………6分
上为减函数。…………………6分
证明:设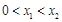 ,则
,则

………10分
∵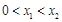
∴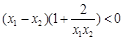 ,即
,即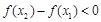 ,即,
,即,
∴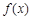 在
在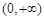 上为减函数。…………………12分
上为减函数。…………………12分
解:(1)由
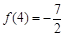 得:
得: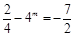 ,即:
,即: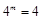 ,解得:
,解得: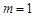 ;…………4分
;…………4分(2) 函数
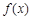 在
在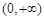 上为减函数。…………………6分
上为减函数。…………………6分证明:设
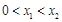 ,则
,则
………10分
∵
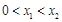
∴
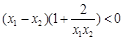 ,即
,即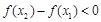 ,即,
,即,
∴
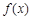 在
在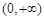 上为减函数。…………………12分
上为减函数。…………………12分
练习册系列答案
相关题目
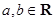 ,具有性质:
,具有性质: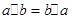 ;②
;②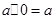 ;③
;③ 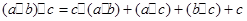 ,
,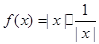 的最小值为 .
的最小值为 . ,有下列结论:①
,有下列结论:① ,函数
,函数 是偶函数; ②
是偶函数; ② ,使得方程
,使得方程 有两个不等实数根; ③
有两个不等实数根; ③ ,若
,若 ,则一定有
,则一定有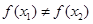 ;④
;④ ,使得函数
,使得函数 在
在 上有三个零点。
上有三个零点。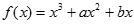 在
在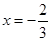 与
与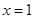 处都取得极值。
处都取得极值。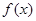 的解析式;(2)求函数
的解析式;(2)求函数
 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当 时,
时, .
. 的值;(2)求证:
的值;(2)求证: 是R上的增函数;
是R上的增函数; ,不等式
,不等式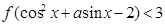 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,将函数
,将函数 的图像向右平移m个单位(m
的图像向右平移m个单位(m ),所的图像对应的函数为奇函数,则m的最小值是( )
),所的图像对应的函数为奇函数,则m的最小值是( )

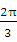

 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线 对称,则函数
对称,则函数 的解析式为
的解析式为



 ,则
,则