题目内容
16.已知f(x)=$\left\{\begin{array}{l}{a^x},(x>1)\\(4-\frac{a}{2})x+2,(x≤1)\end{array}$是R上的单调递增函数,求实数a的取值范围.分析 若分段函数f(x)=$\left\{\begin{array}{l}{a^x},(x>1)\\(4-\frac{a}{2})x+2,(x≤1)\end{array}$是R上的单调递增函数,则每一段均为增函数,且当x=1时,左段函数值不大于右段函数值,进而可得实数a的取值范围.
解答 解:根据函数$f(x)=\left\{\begin{array}{l}{a^x},(x>1)\\(4-\frac{a}{2})x+2,(x≤1)\end{array}\right.$是R上的单调递增函数,
可得:每一段均为增函数,且当x=1时,左段函数值不大于右段函数值,
所以$\left\{{\begin{array}{l}{a>1}\\{4-\frac{a}{2}>0}\\{{a^1}≥({4-\frac{a}{2}})•1+2}\end{array}}\right.⇒4≤a<8$,
故实数a的取值范围为[4,8).
点评 本题考查的知识点是分段函数的单调性,熟练掌握并正确理解分段函数的单调性的实际含义,是解答的关键.

练习册系列答案
相关题目
6.函数f(x)=-x3+ax在[0,+∞)上是减函数,则a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
4.函数f(x)=sinx-2x在区间[0,2π]上的最小值是( )
| A. | -4π | B. | 0 | C. | -2π | D. | 1-π |
6.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=($\frac{1}{2}$)x,x∈R | B. | y=$\frac{1}{x-1}$,x≠1 | C. | y=x+sinx,x∈R | D. | y=-x3-x,x∈R |
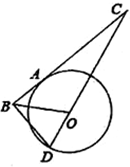 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.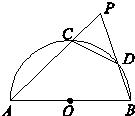 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.