题目内容
7.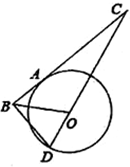 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.(Ⅰ)求证:直线BC是⊙O的切线;
(Ⅱ)若AB=$\sqrt{5}$,DO=2,求BO的长.
分析 (Ⅰ)延长BD到E,使DE=DC,连结CE、AD、AO,证明BD∥AO,AO⊥BC,即可证明直线BC是⊙O的切线;
(Ⅱ)延长BO交⊙O于F,设BO交⊙O于G,由(Ⅰ)得AB2=BG•BF=(BO-DO)(BO+DO),即可求BO的长.
解答 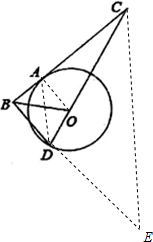 (Ⅰ)证明:延长BD到E,使DE=DC,连结CE、AD、AO.
(Ⅰ)证明:延长BD到E,使DE=DC,连结CE、AD、AO.
∴∠E=∠DCE,∠OAD=∠ODA.…(1分)
∵$\frac{BA}{AC}$=$\frac{DB}{DC}$,∴$\frac{BA}{AC}$=$\frac{DB}{DE}$,
∴AD∥CE.…(2分)
∴∠E=∠ADB,∠ODA=∠DCE,
∴∠ODA=∠ADB.…(3分)
∴∠BAD=∠OAD.
∴BD∥AO.…(4分)
∵BD⊥BC,
∴AO⊥BC,…(5分)
∴直线BC是⊙O的切线.…(6分)
(Ⅱ)解:延长BO交⊙O于F,设BO交⊙O于G.
由(Ⅰ)得AB2=BG•BF=(BO-DO)(BO+DO),…(8分)
∵AB=$\sqrt{5}$,DO=2,
∴($\sqrt{5}$)2=BO2-22,…(9分)
解得,BO=3.…(10分)
点评 本题考查直线与圆的位置关系,考查切割线定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.某同学为了解秋冬季节用电量(y度)与气温(x℃)的关系,由如表数据计算出回归直线方程为y=-2x+60,则表中a的值为38.
| 气温 | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | a | 64 |
12.设x,y∈R,若x-|y|>0,则下列不等式中正确的是( )
| A. | $\frac{1}{x}$<$\frac{1}{y}$ | B. | $\frac{1}{x}$>$\frac{1}{y}$ | C. | x2<y2 | D. | x2>y2 |
19.函数y=x3-3x2-9x(-2<x<2)有( )
| A. | 极大值5,无极小值 | B. | 极小值-27,无极大值 | ||
| C. | 极大值5,极小值-27 | D. | 极大值5,极小值-11 |
17.在△ABC中,若tan A•tan B<1,则△ABC的形状是( )
| A. | 锐角三角形 | |
| B. | 直角三角形 | |
| C. | 钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |