题目内容
【题目】已知椭圆![]() 右焦点
右焦点![]() ,离心率为
,离心率为![]() ,过
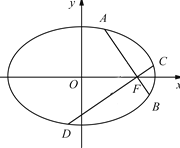
,过![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() ,设
,设![]() 中点分别为
中点分别为![]() .
.
(1) 求椭圆的标准方程;
(2)求以![]() 为顶点的四边形的面积的取值范围;
为顶点的四边形的面积的取值范围;
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(Ⅰ)利用椭圆的离心率![]() ,以及
,以及![]() 求出a、b,即可求椭圆的方程;
求出a、b,即可求椭圆的方程;
(Ⅱ)①当两条弦中一条斜率为0时,另一条弦的斜率不存在,直接求出面积.
②当两弦斜率均存在且不为0时,设A(x1,y1),B(x2,y2),且设直线AB的方程为y=k(x-1),与椭圆方程联立,利用韦达定理以及弦长公式,求出AB,CD即可求解面积的表达式,通过基本不等式求出面积的最值.
解:(1) 由题意:![]() ,
,
∴![]() ,
,
则椭圆的方程为![]()
(2) ①当两直线一条斜率不存在一条斜率为0时, ![]()
②当两直线斜率存在且都不为0时,
设直线![]() 方程为
方程为![]()
将其带入椭圆方程整理得:![]()
![]()
![]()
同理,![]()

![]() ,当
,当![]() 时,
时,![]()
综上所述四边形面积范围是![]()

 阅读快车系列答案
阅读快车系列答案【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线l和曲线![]() 的普通方程;
的普通方程;
(2)设直线l和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
【题目】沃尔玛超市委托某机构调查该超市的顾客使用移动支付的情况.调查人员从年龄在![]() 内的顾客中,随机抽取了200人,调查结果如图所示:
内的顾客中,随机抽取了200人,调查结果如图所示:

(1)为推广移动支付,超市准备对使用移动支付的每位顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关.
的把握认为使用移动支付与年龄有关.
|
| 总计 | |
使用移动支付 | |||
不使用移动支付 | |||
总计 |
 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 | /tr>
| 3.841 | 6.635 | 10.828 |
【题目】某高校“统计”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表,为了判断主修统计专业是否与性别有关,计算得到![]() ,因为
,因为![]() ,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
专业 性别 | 非统计专业 | 统计专业 |
男 | 13 | 10 |
女 | 7 | 20 |
本题可以参考独立性检验临界值表:
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着网络和智能手机的普及与快速发展,许多可以解答各学科问题的搜题软件走红.有教育工作者认为:网搜答案可以起到拓展思路的作用,但是对多数学生来讲,容易产生依赖心理,对学习能力造成损害.为了了解网络搜题在学生中的使用情况,某校对学生在一周时间内进行网络搜题的频数进行了问卷调查,并从参与调查的学生中抽取了男、女学生各![]() 人进行抽样分析,得到如下样本频数分布表:
人进行抽样分析,得到如下样本频数分布表:
一周时间内进行网络搜题的频数区间 | 男生频数 | 女生频数 |
| 18 | 4 |
| 10 | 8 |
| 12 | 13 |
| 6 | 15 |
| 4 | 10 |
将学生在一周时间内进行网络搜题频数超过![]() 次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.
次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.
(1)根据已有数据,完成下列![]() 列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过
列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过![]() %的前提下有把握认为使用网络搜题与性别有关?
%的前提下有把握认为使用网络搜题与性别有关?
经常使用网络搜题 | 偶尔或不用络搜题 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法每次抽取一个人,抽取![]() 人,记经常使用网络搜题的人数为
人,记经常使用网络搜题的人数为![]() ,若每次抽取的结果是相互独立的,求随机变量
,若每次抽取的结果是相互独立的,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
