题目内容
【题目】已知函数![]() 在
在![]() 上没有最小值,则
上没有最小值,则![]() 的取值范围是________________.
的取值范围是________________.
【答案】![]()
【解析】
先求导,利用f′(x)=0时,x=0或x=![]() ,讨论两个极值点与(-1,1)的关系,再根据导数和函数的单调性最值的关系将极值与端点处函数值作比较得到a的范围.
,讨论两个极值点与(-1,1)的关系,再根据导数和函数的单调性最值的关系将极值与端点处函数值作比较得到a的范围.
∵f(x)=x3﹣ax,∴f′(x)=3x2﹣2ax=x(3x-2a),当f′(x)=0时,x=0或x=![]() ,
,
(1)当![]() ∈(﹣∞,﹣1]时,即a
∈(﹣∞,﹣1]时,即a![]() 时,f(x)在(-1,0)单调递减,在(0,1)单调递增,此时x=0时f(x)取得最小值,所以舍去.
时,f(x)在(-1,0)单调递减,在(0,1)单调递增,此时x=0时f(x)取得最小值,所以舍去.
(2)当-1<![]() <0时,f(x)在(-1,
<0时,f(x)在(-1,![]() )单调递增,在(
)单调递增,在(![]() ,0)单调递增减,在(0,1)单调递增,由题意
,0)单调递增减,在(0,1)单调递增,由题意![]() 在
在![]() 上没有最小值,
上没有最小值,
则有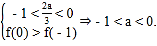
(3)当a=0时,f(x)=![]() 在
在![]() 上显然没有最小值,故成立.
上显然没有最小值,故成立.
(4)当0<![]() <1时,f(x)在(-1,
<1时,f(x)在(-1,![]() )单调递增,在(0,
)单调递增,在(0,![]() )单调递增减,在(
)单调递增减,在(![]() ,1)单调递增,由题意
,1)单调递增,由题意![]() 在
在![]() 上没有最小值,
上没有最小值,
则有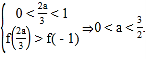
(5)当![]() 时,即a
时,即a![]() 时,f(x)在(-1,0)单调递增,在(0,1)单调递减,
时,f(x)在(-1,0)单调递增,在(0,1)单调递减,
此时f(x)在![]() 上没有最小值.
上没有最小值.
综上:a>-1.
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目