题目内容
【题目】以直角坐标系的原点
为极点，
轴的正半轴为极轴建立极坐标系，已知点
的直角坐标为
，若直线
的极坐标方程为
，曲线
的参数方程是
（
为参数）．
（1）求直线l和曲线的普通方程；
（2）设直线l和曲线交于
两点，求
．
【答案】（1）
和
；（2）1
【解析】
（1）直线的极坐标方程为
，利用互化公式，能求出直线
的普通方程，曲线
的参数方程利用代入法消去参数能求出曲线的普通方程；（2）点
的直角坐标为
，点在直线上，求出直线的参数方程，得到
，由此利用韦达定理，结合直线参数方程的几何意义，能求出
的值.
（1）因为
，所以
由
，得
，因为
消去t得
所以直线l和曲线的普通方程分别为和．
（2）点的直角坐标为
，点在直线l上，设直线的参数方程：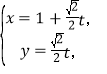
（t为参数），
对应的参数为
． 
练习册系列答案
相关题目
【题目】
是指空气中直径小于或等于
微米的颗粒物（也称可入肺颗粒物）.为了探究车流量与的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与的数据如下表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 |
|
|
|
|
|
|
|
|
|
|
|
（Ⅰ）根据上表数据，请在所给的坐标系中画出散点图；
（Ⅱ）根据上表数据，用最小二乘法求出
关于
的线性回归方程
；
（Ⅲ）若周六同一时间段的车流量是
万辆，试根据（Ⅱ）求出的线性回归方程，预测此时的浓度为多少（保留整数）？
参考公式：由最小二乘法所得回归直线的方程是：，
其中
．
