题目内容
17.在△ABC中,角 A,B,C所对边的长分别为a,b,c,且sinC=2sin(A-B).(Ⅰ)证明:tanA=3tanB;
(Ⅱ)若c=2b=2,求△ABC的面积.
分析 (Ⅰ)由三角形的内角和可得sinC=sin(A+B)=2sin(A-B),由和差角公式展开化简可得;
(Ⅱ)由正、余弦定理及sinAcosB=3cosAsinB结合已知可得a的值,进而可三角形的面积.
解答 解:(Ⅰ)证明:∵A+B+C=π,∴C=π-(A+B),
∴sinC=sin(A+B)=2sin(A-B),
由和差角公式可得sinAcosB+cosAsinB=2sinAcosB-2cosAsinB,
∴sinAcosB=3cosAsinB,∴tanA=3tanB;
(Ⅱ)由正、余弦定理及sinAcosB=3cosAsinB,
得a•$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=3b•$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,
化简代入c=2b=2得a=$\sqrt{3}$,∴△ABC为直角三角形,
∴△ABC的面积S△ABC=$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查正余弦定理,涉及三角形的面积公式和和差角的三角函数公式,属基础题.

练习册系列答案
相关题目
7.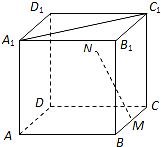 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
12.若函数f(x)满足f(2)=1且f(x+3)=2f(x),则f(2015)=( )
| A. | 2670 | B. | 2671 | C. | 2672 | D. | 2673 |
2.如图所示,程序框图(算法流程图)的输出结果为( )
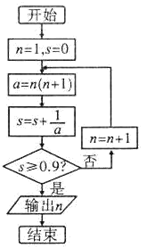

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
9.椭圆ax2+by2=1与直线y=1-x交于A、B两点,过原点与线段AB中点的直线的斜率为$\frac{\sqrt{3}}{2}$,则$\frac{b}{a}$值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{27}$ |
6.已知抛物线y2=4x上两个动点B、C和点A(1,2),且∠BAC=90°,则动直线BC必过定点( )
| A. | (2,5) | B. | (-2,5) | C. | (5,-2) | D. | (5,2) |
7.已知F1、F2为椭圆的两个焦点,以线段F1F2为一边的正方形ABF2F1与椭圆交于M,N两点,且M,N分别为边AF1,BF2的中点,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |