题目内容
7．已知F1、F2为椭圆的两个焦点，以线段F1F2为一边的正方形ABF2F1与椭圆交于M，N两点，且M，N分别为边AF1，BF2的中点，则椭圆的离心率为（ ）| A． | $\sqrt{3}$-1 | B． | $\sqrt{5}$-1 | C． | $\frac{\sqrt{3}-1}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
分析 通过连结MF2，易得MF1=c，利用勾股定理及椭圆定义计算即得结论．
解答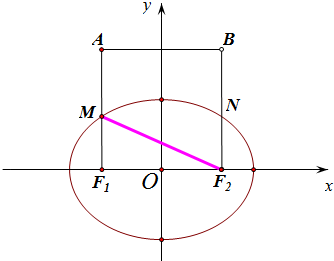 
解：连结MF2，如图，则正方形ABF2F1的边长为2c，
∵M，N分别为边AF1，BF2的中点，∴MF1=c，
由勾股定理可知：MF2=$\sqrt{M{{F}_{1}}^{2}+{F}_{1}{{F}_{2}}^{2}}$=$\sqrt{{c}^{2}+（2c）^{2}}$=$\sqrt{5}$c，
由椭圆定义可知：2a=MF1+MF2=（1+$\sqrt{5}$）c，
∴离心率e=$\frac{c}{a}$=$\frac{c}{\frac{1}{2}（1+\sqrt{5}）c}$=$\frac{\sqrt{5}-1}{2}$，
故选：D．
点评 本题考查求椭圆的离心率，涉及勾股定理等基础知识，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
18．已知命题p：?x∈R，2x-1＞0，则命题?p为（ ）
| A． | ?x∈R，2x-1≤0 | B． | ?x∈R，2x-1≤0 | C． | ?x∈R，2x-1＜0 | D． | ?x∈R，2x-1＜0 |
15．下列命题中：
①若a∈R，则ai是纯虚数；
②若a，b∈R且a＞b，则a+i4＞b+i2；
③复数2+i的模为3；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
①若a∈R，则ai是纯虚数；
②若a，b∈R且a＞b，则a+i4＞b+i2；
③复数2+i的模为3；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
| A． | ①② | B． | ②④ | C． | ②③ | D． | ①④ |
2．某几何体的三视图如图所示，按图中所给的尺寸，该几何体的体积为（ ）
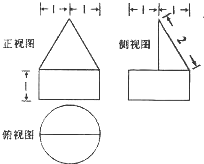
| A． | $\frac{\sqrt{3}π}{6}$+1 | B． | $\frac{\sqrt{3}π}{6}$+π | C． | $\frac{\sqrt{3}π}{3}$+π | D． | $\frac{\sqrt{3}π}{3}$+1 |
12．已知角α的终边经过点P（-b，4）且cosα=-$\frac{3}{5}$，则b的值等于（ ）
| A． | 3 | B． | -3 | C． | ±3 | D． | 5 |
正方形ABCD与正方形ABEF互相垂直，点M，N，G分别是AE，BC，CE的中点，AB=2，