题目内容

12．若函数f（x）满足f（2）=1且f（x+3）=2f（x），则f（2015）=（　　）
A．2670B．2671C．2672D．2673

分析 令x=n，n∈N*代入已知的式子，利用等比数列的定义、通项公式求出f（2015）的值．

解答 解：∵f（x+3）=2f（x），且f（2）=1，
∴令x=n，n∈N*，f（n+3）=2f（n），f（2）=1，
∴f（2）、f（5）、f（8）、…、f（3n-1）是以1为首项，2为公比的等比数列，
∴f（2015）=f（3×672-1）=1•2672-1=2671，
故选：B．

点评 本题考查了等比数列的定义、通项公式，是函数与数列的综合题，属于中档题．

练习册系列答案
相关题目
2．已知正方体ABCD-A1B1C1D1，点E，F，G分别是线段B1B，AB和A1C上的动点，观察直线CE与D1F，CE与D1G．给出下列结论：
①对于任意给定的点E，存在点F，使得D1F⊥CE；
②对于任意给定的点F，存在点E，使得CE⊥D1F；
③对于任意给定的点E，存在点G，使得D1G⊥CE；
④对于任意给定的点G，存在点E，使得CE⊥D1G．
其中正确结论的个数是（　　）
A．1个B．2个C．3个D．4个
3．设p：f（x）=ex+lnx+$\frac{1}{2}$x2+mx+2在（0，+∞）内单调递增，q：m≥-4，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
20．如图，正方体ABC-A1B1C1D1中，点F为A1D的中点．
（Ⅰ）求证：A1B∥平面AFC；
（Ⅱ）求证：平面A1B1D⊥平面AFC．
7．设i是虚数单位，复数$\frac{{-2\sqrt{3}+i}}{{1+2\sqrt{3}i}}$=（　　）
A．-1B．1C．-iD．i
17．在△ABC中，角 A，B，C所对边的长分别为a，b，c，且sinC=2sin（A-B）．
（Ⅰ）证明：tanA=3tanB；
（Ⅱ）若c=2b=2，求△ABC的面积．
4．设Sn是等差数列{an}的前n项和，且a2+2a4+5a6=32，则S9=36．
1．已知定义在R上的函数f（x）满足f（1）=1，且对于任意的x，f′（x）$＜\frac{1}{2}$恒成立，则不等式f（lg2x）＜$\frac{l{g}^{2}x}{2}$+$\frac{1}{2}$的解集为（　　）
A．（0，$\frac{1}{10}$）B．（10，+∞）C．（$\frac{1}{10}$，10）D．（0，$\frac{1}{10}$）∪（10，+∞）
2．某几何体的三视图如图所示，按图中所给的尺寸，该几何体的体积为（　　）
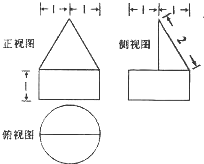
A．$\frac{\sqrt{3}π}{6}$+1B．$\frac{\sqrt{3}π}{6}$+πC．$\frac{\sqrt{3}π}{3}$+πD．$\frac{\sqrt{3}π}{3}$+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网