题目内容
8.由直线x-y+1=0,x+y-5=0和x-1=0所围成的三角形区域(包括边界)用不等式组可表示为( )| A. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
分析 作出对应的三角形区域,判断区域和直线的位置关系即可得到结论.
解答 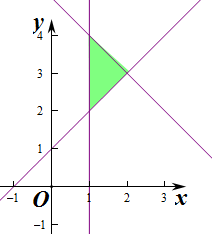 解:作出对应的三角形区域,
解:作出对应的三角形区域,
则区域在直线x-1=0的右侧,满足x≥1,
在x-y+1=0的上方,满足x-y+1≤0,
则x+y-5=0的下方,满足x+y-5≤0,
故对应的不等式组为$\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$,
故选:A.
点评 本题主要考查二元一次不等式组表示平面区域,比较基础.

练习册系列答案
相关题目
3.直线2y+2x-5=0的倾斜角是( )
| A. | 45° | B. | 135° | C. | 120° | D. | 150° |
13.设函数f(x)=sinx+cosx,把f(x)的图象向右平移m(m>0)个单位长度后图象恰好为函数g(x)=sinx-cosx的图象,则m的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
20. 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | 16π | D. | 8π |
17.已知i为虚数单位,且z=i(1-i),则复数z的共轭复数为( )
| A. | -1+i | B. | 1-i | C. | 1+i | D. | -1-i |