题目内容
5.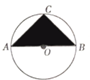 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
分析 由题意,本题是几何概型的概率,所以只要求出阴影部分的面积与圆面积的比即可.
解答 解:本题是几何概型的考查,设圆的半径为r,则阴影部分的面积为$\frac{1}{2}×2r×r={r}^{2}$,圆的面积为πr2,
由几何概型的概率公式可求黄豆落到阴影部分的概率为:$\frac{{r}^{2}}{π{r}^{2}}=\frac{1}{π}$;
故答案为:$\frac{1}{π}$.
点评 本题考查了几何概型概率的求法;只要正确的选择事件的测度(长度,面积,体积),利用测度比求概率.

练习册系列答案
相关题目
13.设函数f(x)=sinx+cosx,把f(x)的图象向右平移m(m>0)个单位长度后图象恰好为函数g(x)=sinx-cosx的图象,则m的最小值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
20. 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
 某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图是边长为4的正方形,侧视图是矩形,俯视图是半圆,则该几何体的体积为( )| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | 16π | D. | 8π |
10.设Sn是公差不为0的等差数列{an}的前n项和,S3=a22,且S1,S2,S4成等比数列,则a10=( )
| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
17.已知i为虚数单位,且z=i(1-i),则复数z的共轭复数为( )
| A. | -1+i | B. | 1-i | C. | 1+i | D. | -1-i |
14.甲、乙两人分别从四种不同品牌的商品中选择两种,则甲、乙所选的商品中恰有一种品牌相同的选法种数是( )
| A. | 30 | B. | 24 | C. | 12 | D. | 6 |
11.设命题p:?x∈R,x2+x+1<0;命题q:?x∈[1,2],x2-1≥0;则以下命题是真命题的是( )
| A. | ¬p∧¬q | B. | p∨¬q | C. | ¬p∧q | D. | p∧q |