题目内容
已知向量p=(an,2n),q=(2n+1,-an+1),n∈N*,p与q垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
(1)2n-1(2)Sn=1+(n-1)2n
(1)∵向量p与q垂直,
∴2nan+1-2n+1an=0,即2nan+1=2n+1an,
∴ =2,∴{an}是以1为首项,2为公比的等比数列,
=2,∴{an}是以1为首项,2为公比的等比数列,
∴an=2n-1.
(2)∵bn=log2an+1,∴bn=n,∴an·bn=n·2n-1,
∴Sn=1+2·2+3·22+4·23+…+n·2n-1,①
∴2Sn=1·2+2·22+3·23+4·24+…+n·2n,②
∴由①-②得,
-Sn=1+2+22+23+24+…+2n-1-n·2n=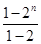 -n·2n=(1-n)2n-1,
-n·2n=(1-n)2n-1,
∴Sn=1+(n-1)2n.
∴2nan+1-2n+1an=0,即2nan+1=2n+1an,
∴
 =2,∴{an}是以1为首项,2为公比的等比数列,
=2,∴{an}是以1为首项,2为公比的等比数列,∴an=2n-1.
(2)∵bn=log2an+1,∴bn=n,∴an·bn=n·2n-1,
∴Sn=1+2·2+3·22+4·23+…+n·2n-1,①
∴2Sn=1·2+2·22+3·23+4·24+…+n·2n,②
∴由①-②得,
-Sn=1+2+22+23+24+…+2n-1-n·2n=
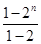 -n·2n=(1-n)2n-1,
-n·2n=(1-n)2n-1,∴Sn=1+(n-1)2n.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,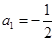 ,
,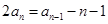
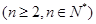 ,设
,设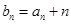 .
.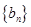 是等比数列;
是等比数列;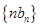 的前
的前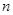 项和
项和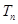 ;
;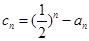 ,
,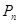 为数列
为数列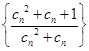 的前
的前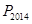 的最大的整数.
的最大的整数.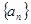 的前
的前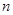 项和
项和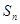 满足
满足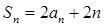
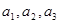 ;
;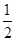 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.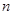 为正整数,由数列
为正整数,由数列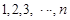 分别求相邻两项的和,得到一个有
分别求相邻两项的和,得到一个有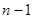 项的新数列;1+2,2+3,3+4,
项的新数列;1+2,2+3,3+4,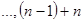 即3,5,7,
即3,5,7,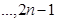 . 对这个新数列继续上述操作,这样得到一系列数列,最后一个数列只有一项.⑴记原数列为第一个数列,则第三个数列的第2项是______⑵最后一个数列的项是___________.
. 对这个新数列继续上述操作,这样得到一系列数列,最后一个数列只有一项.⑴记原数列为第一个数列,则第三个数列的第2项是______⑵最后一个数列的项是___________.