题目内容
【题目】某农场种植黄瓜,根据多年的市场行情得知,从春节起的300天内,黄瓜市场售价与上市时间的关系用图1所示的一条折线表示,黄瓜的种植成本与上市时间的关系用图2所示的抛物线表示.(注:市场售价和种植成本的单位:元/kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(x);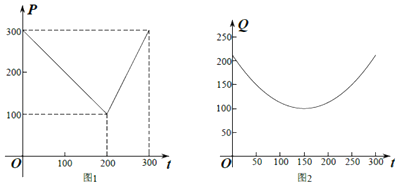
(2)认定市场售价减去种植成本为纯收益,问从春节开始的第几天上市的黄瓜纯收益最大?并求出最大值.
【答案】
(1)解:由图1可得市场售价与时间的函数关系为f(t)= ![]() ,
,
由图2可得种植成本与时间的函数关系式为g(t)= ![]() (t﹣150)2+100,0≤t≤300
(t﹣150)2+100,0≤t≤300
(2)解:设t时刻的纯收益为h(t),则h(t)=f(t)﹣g(t),
即h(t)= 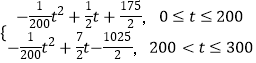 ,
,
当0≤t≤200时,配方整理得h(t)=﹣ ![]() (t﹣50)2+100,
(t﹣50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得h(t)=﹣ ![]() (t﹣350)2+100,
(t﹣350)2+100,
所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5;
综上所述,纯收益最大值为100元,此时t=50,即从二月一日开始的第50天时,上市的西红柿收益最答.
【解析】1、本题考查的是一次函数的图像问题,由待定系数法求出分段函数的两个解析式。
2、由题意可得设t时刻的纯收益为h(t),则h(t)=f(t)﹣g(t)得到函数的解析式,当0≤t≤200时,配方整理得h(t)=﹣ 1 200 (t﹣50)2+100,所以,当t=50时,h(t)取得区间[0,200]上的最大值100;当200<t≤300时,配方整理得h(t)=﹣ ![]() (t﹣350)2+100,
(t﹣350)2+100,
所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5
综上所述,纯收益最大值为100元,此时t=50,即从二月一日开始的第50天时,上市的西红柿收益最答
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案