题目内容
【题目】己知圆C1的参数方程为 ![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2 ![]() cos(θ﹣
cos(θ﹣ ![]() ). (Ⅰ)将圆C1的参数方程他为普通方程,将圆C2的极坐标方程化为直角坐标方程;
). (Ⅰ)将圆C1的参数方程他为普通方程,将圆C2的极坐标方程化为直角坐标方程;
(Ⅱ)圆C1 , C2是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
【答案】解:(I)由圆C1的参数方程 ![]() , 消去参数φ可得:x2+y2=1.
, 消去参数φ可得:x2+y2=1.
由圆C2的极坐标方程ρ=2 ![]() cos(θ﹣
cos(θ﹣ ![]() ),化为
),化为 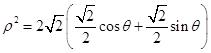 ρ,
ρ,
∴x2+y2=2x+2y.即(x﹣1)2+(y﹣1)2=2.
(II)由x2+y2=1,x2+y2=2x+2y.可得两圆的相交弦所在的直线方程为2x+2y=1.
圆心(0,0)到此直线的距离d= ![]() =
= ![]() .
.
∴弦长|AB|=2 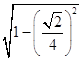 =
= ![]()
【解析】(I)利用sin2φ+cos2φ=1即可把圆C1的参数方程 ![]() ,化为直角坐标方程.(II)由x2+y2=1,x2+y2=2x+2y.可得两圆的相交弦所在的直线方程为2x+2y=1.利用点到直线的距离公式可得圆心(0,0)到此直线的距离d,即可得出弦长|AB|=2
,化为直角坐标方程.(II)由x2+y2=1,x2+y2=2x+2y.可得两圆的相交弦所在的直线方程为2x+2y=1.利用点到直线的距离公式可得圆心(0,0)到此直线的距离d,即可得出弦长|AB|=2 ![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
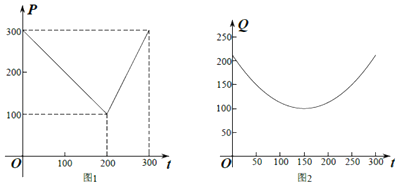
活力试卷系列答案【题目】光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
第t天 | 10 | 17 | 21 | 30 |
Q(件) | 180 | 152 | 136 | 100 |
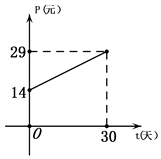
(1)根据图象写出销售价格与时间t的函数关系式P=f(t).
(2)请根据表中数据写出日销售量Q与时间t的函数关系式Q=g(t).
(3)设日销售额为M(单位:元),请求出这30天中第几日M最大,最大值为多少?