题目内容
【题目】已知f（x）是定义在R上的奇函数，当x∈[0，+∞）时，f（x）=2x+x﹣m（m为常数）．
（1）求常数m的值．
（2）求f（x）的解析式．
（3）若对于任意x∈[﹣3，﹣2]，都有f（k4x）+f（1﹣2x+1）＞0成立，求实数k的取值范围．
【答案】
（1）解：∵f（x）是奇函数，且定义域为R；
∴f（0）=0；
∵当x≥0时，f（x）=2x+x﹣m（m为常数）；
∴f（0）=1﹣m，∴1﹣m=0；
∴m=1
（2）解：由（1）知，m=1；
∴当x≥0时，f（x）=2x+x﹣1；
设x＜0，则﹣x＞0，且f（x）为奇函数，所以：
f（﹣x）=2﹣x﹣x﹣1=﹣f（x）；
∴f（x）=﹣2﹣x+x+1；
∴ 
（3）解：因为当x变大时，2x变大，x﹣1变大，所以2x+x﹣1的值也变大；
所以f（x）在[0，+∞）上是增函数且左端点为原点；
因为，f（x）是奇函数，且f（0）=0；
所以f（x）在（﹣∞，0）上也是增函数，且右端点是原点；
所以f（x）在R上是增函数；
∵f（x）是奇函数；
∴f（k4x）+f（1﹣2x+1）＞0等价于f（k4x）＞﹣f（1﹣2x+1），等价于f（k4x）＞f（﹣1+2x+1）；
∵f（x）在R上是增函数；
∴f（k4x）＞f（﹣1+2x+1）等价于k4x＞﹣1+2x+1；
∵4x＞0∴k4x＞﹣1+2x+1等价于 
；
∴f（k4x）+f（1﹣2x+1）＞0对x∈[﹣3，﹣2]恒成立等价于 
；
设y= 
；
∴ 
= 
；
x∈[﹣3，﹣2]，∴ 
；
∴ 
时，y取最大值﹣8；
∴k＞﹣8；
即实数k的取值范围为（﹣8，+∞）．
【解析】1、本题考查的是奇函数的定义，且定义域为R∴f（0）=0，再由特殊之法求得m=1。
2、当x≥0时，f（x）=2x+x﹣1；x＜0，则﹣x＞0，且f（x）为奇函数，所以f（﹣x）=2﹣x﹣x﹣1=﹣f（x）∴f（x）=﹣2﹣x+x+1；即得函数的解析式。
3、由增函数的定义可得f（x）在R上是增函数∵f（x）是奇函数可得f（k4x）＞f（﹣1+2x+1），根据增减性可得不等式k4x＞﹣1+2x+1 ∴f（k4x）+f（1﹣2x+1）＞0对x∈[﹣3，﹣2]恒成立，整理得
， x ∈ [ 3 ， 2 ].整理得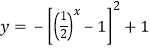
,x∈[﹣3，﹣2]，
∴ 
x ∈ [ 4 ， 8 ] ，当=4时，y取最大值﹣8∴k＞﹣8
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点，需要掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能正确解答此题．
