题目内容
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 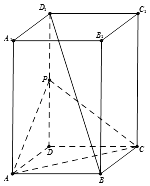
(1)求证:直线BD1∥平面PAC
(2)求证:平面PAC⊥平面BDD1B1 .
【答案】
(1)证明:连接BD交AC于O点,连接OP,
因为O为矩形对角线的交点,O为BD的中点,P为DD1的中点,
则OP∥BD1,又因为OP面APC,BD1面APC
所以直线BD1∥平面PAC
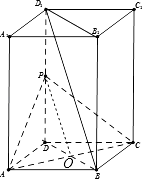
(2)证明:因为AB=AD=1,所以矩形ABCD为正方形,所以AC⊥BD,
由长方体可知,DD1⊥AC,而BD∩DD1=D,
所以AC⊥面BDD1B1,且AC面PAC,
则平面PAC⊥平面BDD1B1
【解析】(1)连接BD交AC于O点,连接OP,运用三角形的中位线定理和线面平行的判定定理,即可得证;(2)由线面垂直的判定定理,证得AC⊥面BDD1B1 , 再由面面垂直的判定定理即可得证.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目