��Ŀ����
1��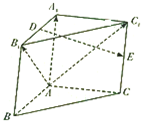 ��ͼ����������ABC-A1B1C1�У�A1A�͵���ABC��AB��AC��E�ֱ���A1B1��CC1���е㣮
��ͼ����������ABC-A1B1C1�У�A1A�͵���ABC��AB��AC��E�ֱ���A1B1��CC1���е㣮�����û�����$\overrightarrow{A{A}_{1}}$��$\overrightarrow{A{B}_{1}}$��$\overrightarrow{A{C}_{1}}$��ʾ����$\overrightarrow{DE}$��
������AB=AC=AA1=1����ֱ��DE��ƽ��AB1C1���ɽǵ�����ֵ��
���� �������������ķֽ�ͺϳɱ�ʾ����$\overrightarrow{DE}$��
�������ռ�ֱ������ϵ��д��������꣬�����������������������������ֵ
��� 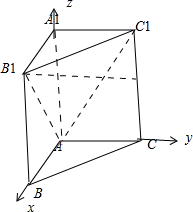 �⣺����$\overrightarrow{DE}=\overrightarrow{D{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}}+\overrightarrow{{C}_{1}E}$=$\frac{1}{2}\overrightarrow{{B}_{1}{A}_{1}}+��\overrightarrow{A{C}_{1}}-\overrightarrow{A{A}_{1}}��-\frac{1}{2}\overrightarrow{A{A}_{1}}$
�⣺����$\overrightarrow{DE}=\overrightarrow{D{A}_{1}}+\overrightarrow{{A}_{1}{C}_{1}}+\overrightarrow{{C}_{1}E}$=$\frac{1}{2}\overrightarrow{{B}_{1}{A}_{1}}+��\overrightarrow{A{C}_{1}}-\overrightarrow{A{A}_{1}}��-\frac{1}{2}\overrightarrow{A{A}_{1}}$
=$\frac{1}{2}��\overrightarrow{A{A}_{1}}-\overrightarrow{A{B}_{1}}��+��\overrightarrow{A{C}_{1}}-\overrightarrow{A{A}_{1}}��-\frac{1}{2}$$\overrightarrow{A{A}_{1}}$
=-$\overrightarrow{A{A}_{1}}-\frac{1}{2}\overrightarrow{A{B}_{1}}+\overrightarrow{A{C}_{1}}$
������ͼ��ʾ�����ռ�ֱ������ϵ�����B1��1��0��1��C1��0��1��1��D��$\frac{1}{2}$��0��1����E��0��1��2��
��$\overrightarrow{n}=��x��y��z��$Ϊƽ��AB1C1�ķ���������$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{A{C}_{1}}=0}\end{array}\right.$
��Ϊ$\overrightarrow{A{B}_{1}}=��1��0��1����\overrightarrow{A{C}_{1}}=��0��1��1��$��$\left\{\begin{array}{l}{x+z=0}\\{y+z=0}\end{array}\right.$��
ȡx=1����$\overrightarrow{n}=��1��1��-1��$
��Ϊ$\overrightarrow{DE}=��-\frac{1}{2}��1��-\frac{1}{2}��$����$cos��\overrightarrow{DE}��\overrightarrow{n}��=\frac{\overrightarrow{DE}•\overrightarrow{n}}{|\overrightarrow{DE}||\overrightarrow{n}|}=\frac{\sqrt{2}}{3}$
����ֱ��DE��ƽ��AB1C1���ɵĽǵ�����ֵΪ$\frac{\sqrt{2}}{3}$
���� ������Ҫ����ռ������ķֽ�ϳɺͿռ�ֱ������ϵ�����弸���е�Ӧ�ã����������͡��е��⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | �٢� | B�� | �ڢ� | C�� | �ۢ� | D�� | �ڢ� |
| A�� | $\frac{��}{2}$ | B�� | �� | C�� | 2�� | D�� | 4�� |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{6}$ |
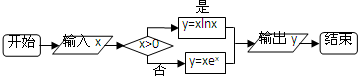
| A�� | [-$\frac{1}{e}$��0] | B�� | [-$\frac{1}{e}$��0�� | C�� | [-$\frac{1}{e}$��+�ޣ� | D�� | [-$\frac{1}{e}$��e�� |
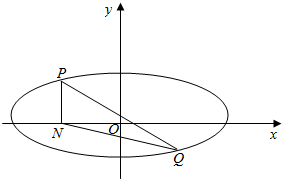 ��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{{\sqrt{3}}}{2}$������ԲC�����㣨0��1����
��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������Ϊ$\frac{{\sqrt{3}}}{2}$������ԲC�����㣨0��1����