题目内容
10.已知复数z1=2+i,z2=m+i,若z1•z2是纯虚数,则m=$\frac{1}{2}$.分析 直接利用复数的乘法运算法则化简,然后利用复数的概念求解即可.
解答 解:复数z1=2+i,z2=m+i,z1•z2=2m-1+(2+m)i,
若z1•z2是纯虚数,
可得m=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查复数的代数形式的混合运算,复数的基本概念的应用,考查计算能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
15.已知△ABC中,角A,B,C所对的边分别为a,b,c,且b+c=8,1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$,则△ABC面积的最大值为( )
| A. | 4 | B. | 4$\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
2.在区域$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$内任意取一点P(x,y),则x2+y2>1的概率是( )
| A. | $\frac{2π-4}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{4-π}{4}$ |
19.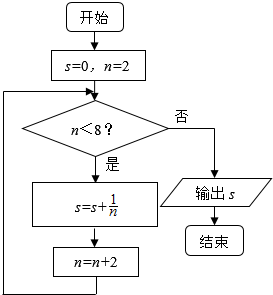 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )
 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )| A. | $\frac{1}{16}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{3}{4}$ |
 (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);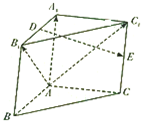 如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.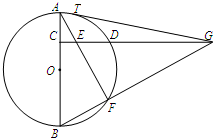 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.