题目内容
9.已知直线l1:ax+2y-1=0,直线l2:x+by-3=0,且l1的倾斜角为$\frac{π}{4}$,则a=-2;若l1⊥l2,则b=1;若l1∥l2,则两直线间的距离为$\frac{7\sqrt{2}}{4}$.分析 由条件根据两条直线平行的条件求出a的值,利用两条直线垂直的条件求出b的值,再利用两条平行直线间的距离公式求得两直线间的距离.
解答 解:由题意可得l1的斜率为tan$\frac{π}{4}$=1=-$\frac{a}{2}$,∴a=-2,直线l1:-2x+2y-1=0.
若l1⊥l2,则1•(-$\frac{1}{b}$ )=-1,∴b=1.
若l1∥l2,则它们的斜率相等,即-$\frac{1}{b}$=1,∴b=-1,
故 l1:-2x+2y-1=0,直线l2:x-y-3=0,即 l1:-2x+2y-1=0,直线l2:-2x+2y+6=0,
两直线间的距离为 $\frac{|6-(-1)|}{\sqrt{4+4}}$=$\frac{7\sqrt{2}}{4}$,
故答案为:-2;1;$\frac{7\sqrt{2}}{4}$.
点评 本题主要考查两条直线平行、垂直的条件,两条平行直线间的距离公式,属于基础题.

练习册系列答案
相关题目
20.下列不等式正确的是( )
| A. | sin1<2sin$\frac{1}{2}<3sin\frac{1}{3}$ | B. | 3sin$\frac{1}{3}<2sin\frac{1}{2}$<sin1 | ||
| C. | sin1<3sin$\frac{1}{3}<2sin\frac{1}{2}$ | D. | 2sin$\frac{1}{2}<sin1<3sin\frac{1}{3}$ |
2.在区域$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$内任意取一点P(x,y),则x2+y2>1的概率是( )
| A. | $\frac{2π-4}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{4-π}{4}$ |
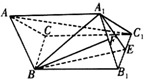 如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.
如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°. (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示); 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,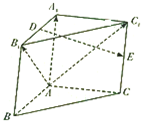 如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,AB⊥AC,E分别是A1B1,CC1的中点.