题目内容
设数列{an}前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值.
(2)求数列{an}的通项公式.
(1)求a1的值.
(2)求数列{an}的通项公式.
(1) a1=1 (2) an=3·2n-1-2,n∈N*
(1)当n=1时,T1=2S1-1.
因为T1=S1=a1,所以a1=2a1-1,解得a1=1.
(2)当n≥2时,Sn=Tn-Tn-1
=2Sn-n2-[2Sn-1-(n-1)2]
=2Sn-2Sn-1-2n+1,所以Sn=2Sn-1+2n-1 ①,
所以Sn+1=2Sn+2n+1 ②,
②-①得an+1=2an+2,
所以an+1+2=2(an+2),
即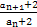 =2(n≥2),
=2(n≥2),
求得a1+2=3,a2+2=6,则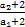 =2.
=2.
所以{an+2}是以3为首项,2为公比的等比数列,
所以an+2=3·2n-1,
所以an=3·2n-1-2,n∈N*.
因为T1=S1=a1,所以a1=2a1-1,解得a1=1.
(2)当n≥2时,Sn=Tn-Tn-1
=2Sn-n2-[2Sn-1-(n-1)2]
=2Sn-2Sn-1-2n+1,所以Sn=2Sn-1+2n-1 ①,
所以Sn+1=2Sn+2n+1 ②,
②-①得an+1=2an+2,
所以an+1+2=2(an+2),
即
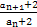 =2(n≥2),
=2(n≥2),求得a1+2=3,a2+2=6,则
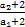 =2.
=2.所以{an+2}是以3为首项,2为公比的等比数列,
所以an+2=3·2n-1,
所以an=3·2n-1-2,n∈N*.

练习册系列答案
相关题目
 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.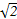 )
)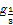 (a5+a7+a9)的值是( )
(a5+a7+a9)的值是( )