题目内容
已知数列{an}的前n项和Sn=n2+1,数列{bn}是首项为1,公比为b的等比数列.
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Tn.
(1) an=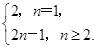 (2) Tn=
(2) Tn=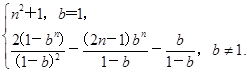
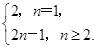 (2) Tn=
(2) Tn=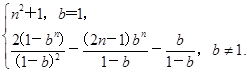
(1)当n=1时,a1=S1=2;当n≥2时,an=Sn-Sn-1=n2+1-(n-1)2-1=2n-1.
所以an=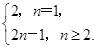
(2)当b=1时,anbn=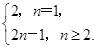
此时,Tn=2+3+5+…+(2n-1)=n2+1.
当b≠1时,anbn=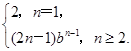
此时,Tn=2+3b+5b2+…+(2n-1)bn-1,①
两端同时乘以b,得bTn=2b+3b2+5b3+…+(2n-1)bn.②
①-②,得(1-b)Tn=2+b+2b2+2b3+…+2bn-1-(2n-1)bn=
2(1+b+b2+b3+…bn-1)-(2n-1)·bn-b=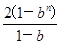 -(2n-1)bn-b,所以Tn=
-(2n-1)bn-b,所以Tn=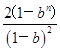 -
-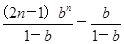 .
.
综上所述,Tn=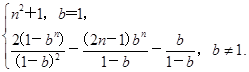
所以an=
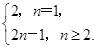
(2)当b=1时,anbn=
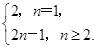
此时,Tn=2+3+5+…+(2n-1)=n2+1.
当b≠1时,anbn=
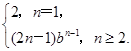
此时,Tn=2+3b+5b2+…+(2n-1)bn-1,①
两端同时乘以b,得bTn=2b+3b2+5b3+…+(2n-1)bn.②
①-②,得(1-b)Tn=2+b+2b2+2b3+…+2bn-1-(2n-1)bn=
2(1+b+b2+b3+…bn-1)-(2n-1)·bn-b=
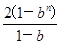 -(2n-1)bn-b,所以Tn=
-(2n-1)bn-b,所以Tn=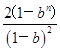 -
-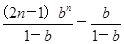 .
.综上所述,Tn=
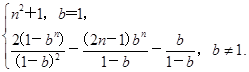

练习册系列答案
相关题目
 +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.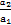 ,
,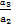 ,…,
,…, ,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )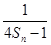 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由. ,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.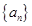 的前
的前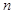 项和
项和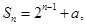 则
则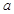 等于( )
等于( )