题目内容
设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对?n∈N*,有S2n<3Sn,则q的取值范围是( )
| A．(0,1] | B．(0,2) | C．[1,2) | D．(0, ) |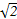
A
若q=1,则S2n=2na1<3na1=3Sn,所以q=1符合要求;当q≠1时,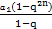
<
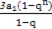,若q>1,则可得q2n-3qn+2<0,即(qn-1)(qn-2)<0,即1<qn<2,而q>1不可能对任意n值都有qn<2,所以q>1不符合要求;当0<q<1时,可得(qn-1)(qn-2)>0,即qn<1,由于0<q<1,所以对任意n值都有qn<1,所以q<1符合要求.综合可得q的取值范围是(0,1].
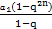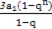<,若q>1,则可得q2n-3qn+2<0,即(qn-1)(qn-2)<0,即1<qn<2,而q>1不可能对任意n值都有qn<2,所以q>1不符合要求;当0<q<1时,可得(qn-1)(qn-2)>0,即qn<1,由于0<q<1,所以对任意n值都有qn<1,所以q<1符合要求.综合可得q的取值范围是(0,1].
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
＋3an＋2，且a1，a2，a6是等比数列{bn}的前三项．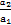
,
,…,
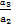,…是首项为1,公比为2的等比数列,则数列{an}的第100项等于( )
，记数列{cn}的前n项和Tn.若对?n∈N*，Tn≤k(n＋4)恒成立，求实数k的取值范围．