题目内容
已知函数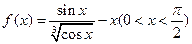 .
.
(1)求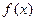 的导数
的导数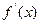 ;
;
(2)求证:不等式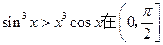 上恒成立;
上恒成立;
(3)求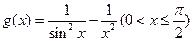 的最大值。
的最大值。
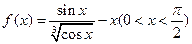 .
.(1)求
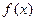 的导数
的导数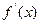 ;
;(2)求证:不等式
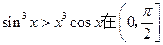 上恒成立;
上恒成立;(3)求
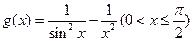 的最大值。
的最大值。(1)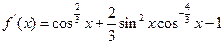 (2)证明见解析 (3)
(2)证明见解析 (3)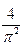
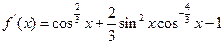 (2)证明见解析 (3)
(2)证明见解析 (3)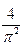
(1)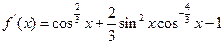 ………………(2分)
………………(2分)
(2).由(1)知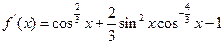 ,其中
,其中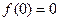
令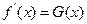 ,对
,对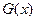 求导数得
求导数得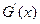
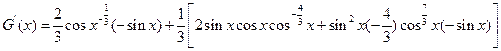
=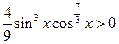 在
在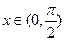 上恒成立.
上恒成立.
故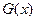 即
即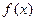 的导函数在
的导函数在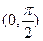 上为增函数,故
上为增函数,故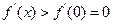
进而知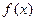 在
在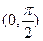 上为增函数,故
上为增函数,故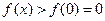
当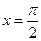 时,
时,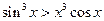 显然成立.
显然成立.
于是有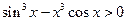 在
在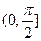 上恒成立.…………………………(9分)
上恒成立.…………………………(9分)
(3)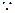 由(2)可知
由(2)可知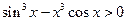 在
在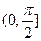 上恒成立.
上恒成立.
则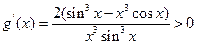 在
在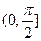 上恒成立.即
上恒成立.即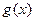 在
在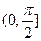 单增
单增
于是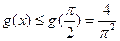 …………………………………………………(12分)
…………………………………………………(12分)
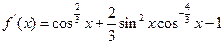 ………………(2分)
………………(2分)(2).由(1)知
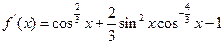 ,其中
,其中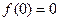
令
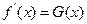 ,对
,对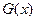 求导数得
求导数得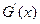
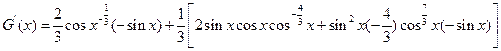
=
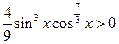 在
在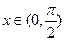 上恒成立.
上恒成立.故
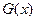 即
即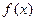 的导函数在
的导函数在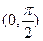 上为增函数,故
上为增函数,故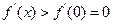
进而知
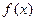 在
在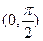 上为增函数,故
上为增函数,故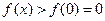
当
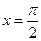 时,
时,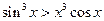 显然成立.
显然成立. 于是有
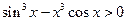 在
在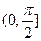 上恒成立.…………………………(9分)
上恒成立.…………………………(9分) (3)
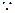 由(2)可知
由(2)可知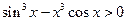 在
在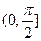 上恒成立.
上恒成立.则
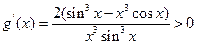 在
在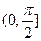 上恒成立.即
上恒成立.即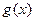 在
在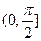 单增
单增 于是
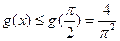 …………………………………………………(12分)
…………………………………………………(12分)
练习册系列答案
相关题目
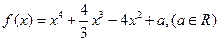 。
。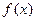 的极大值;
的极大值;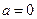 时,求函数
时,求函数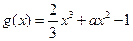 ,当
,当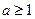 时,
时,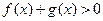 恒成立,求
恒成立,求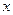 的取值范围。
的取值范围。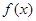 的图象如图所示,则不等式
的图象如图所示,则不等式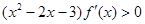 的解集为
的解集为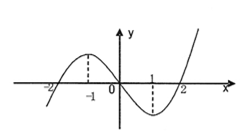




 的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?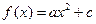 的图象经过点
的图象经过点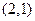 ,且在
,且在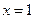 处的切线方程是
处的切线方程是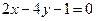
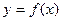 的解析式;
的解析式;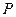 是直线
是直线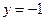 上的动点,自点
上的动点,自点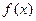 的图象的两条切线
的图象的两条切线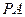 、
、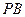 (点
(点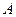 、
、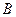 为切点),求证直线
为切点),求证直线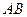 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。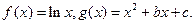
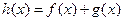 是单调递增函数,求实数
是单调递增函数,求实数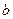 的取值范围;
的取值范围;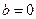 时,两曲线
时,两曲线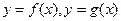 有公共点P,设曲线
有公共点P,设曲线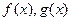 在P处的切线分别为
在P处的切线分别为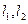 ,若切线
,若切线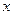 轴围成一个等腰三角形,求P点坐标和
轴围成一个等腰三角形,求P点坐标和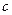 的值;
的值;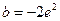 时,讨论关于
时,讨论关于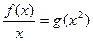 的根的个数
的根的个数
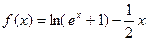 .
.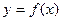 的单调区间,并判断函数的奇偶性;
的单调区间,并判断函数的奇偶性;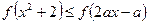 的解集是集合
的解集是集合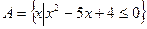 的子集,求实数
的子集,求实数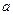 的取值范围.
的取值范围.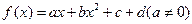 的导函数
的导函数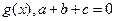 ,且
,且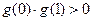 设
设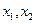 是方程
是方程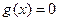 的两根,则|
的两根,则|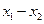 |的取值范围为
|的取值范围为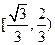 B
B 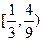 C
C 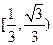 D
D