题目内容
已知定义在R上的可导函数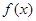 的图象如图所示,则不等式
的图象如图所示,则不等式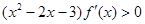 的解集为
的解集为
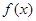 的图象如图所示,则不等式
的图象如图所示,则不等式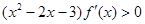 的解集为
的解集为
A. |
B. |
C. |
D. |
D
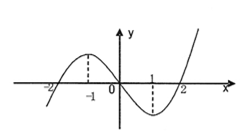
由图可知:
当x∈(-∞,-1)∪(1,∞)时,f’(x)>0
当x∈(-1,1)时,f’(x)<0
因此:
1、当x∈(-∞,-1)∪(1,∞)时:
由(x2-2x-3)f’(x)>0、f’(x)>0
可知:x^2-2x-3>0
即:(x-3)(x+1)>0
有:x-3>0、x+1>0…………(1)
或:x-3<0、x+1<0…………(2)
由(1)得:x>3
由(2)得:x<-1
x的取值范围是:x∈(3,∞),或x∈(-∞,-1)
2、当x∈(-1,1)时:
由(x2-2x-3)f’(x)>0、f’(x)<0
可知:x2-2x-3<0
即:(x-3)(x+1)<0
有:x-3>0、x+1<0…………(1)
或:x-3<0、x+1>0…………(2)
由(1)得:x<-1、x>3,矛盾,舍去。
由(2)得:-1<x<3
考虑此时x∈(-1,1),
所以:x的取值范围是:x∈(-1,1)
综上所述,x的取值范围是:x∈(-∞,-1)∪(-1,1)∪(3,∞)。故选D。

练习册系列答案
相关题目
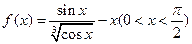 .
.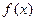 的导数
的导数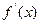 ;
;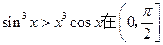 上恒成立;
上恒成立;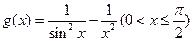 的最大值。
的最大值。 ,且函数
,且函数 的图象关于原点对称,其图象在
的图象关于原点对称,其图象在 处的切线方程为
处的切线方程为 (1)求
(1)求 使得函数
使得函数 的定义域和值域均为
的定义域和值域均为 .
. 时,求
时,求 的单调区间和极值;
的单调区间和极值; ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.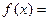
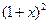 -4
-4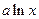 (a∈N﹡).(Ⅰ)若函数
(a∈N﹡).(Ⅰ)若函数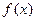 在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程
在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程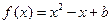 在区间[1,e]上恰有一个实根,求实数b的取值范围.
在区间[1,e]上恰有一个实根,求实数b的取值范围. 函数
函数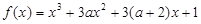 有极值;命题
有极值;命题 函数
函数 且
且 恒成立.若
恒成立.若 为真命题,
为真命题, 为真命题,则
为真命题,则 的取值范围是
的取值范围是




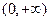 上的三个函数:
上的三个函数: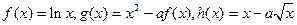 ,已知
,已知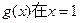 处取极值.
处取极值.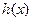 的单调性;
的单调性; 成立.
成立.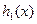 的图象,试确定函数
的图象,试确定函数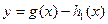 的零点个数,并说明理由。
的零点个数,并说明理由。 =
= 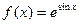 ,则
,则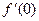 等于
等于


