题目内容
已知函数f(x)=x3-3ax2+2bx在点x=1处有极小值-1,试确定a,b的值,并求出f(x)的单调递增区间.
在f(x)的单调递增区间为区间(-∞,- )和(1,+∞)
)和(1,+∞)
 )和(1,+∞)
)和(1,+∞)由已知,可得f(1)=1-3a+2b=-1. ①
又f′(x)=3x2-6a+2b,
∴f′(1)=3-6a+2b="0. " ② -------------------4分
由①②可得 故函数的解析式为f(x)=x3-x2-x. ----------------8分
故函数的解析式为f(x)=x3-x2-x. ----------------8分
由此得f′(x)=3x2-2x-1.
当f′(x)>0时, x<- 或x>1。
或x>1。
因此在f(x)的单调递增区间为区间(-∞,- )和(1,+∞).
)和(1,+∞).
又f′(x)=3x2-6a+2b,
∴f′(1)=3-6a+2b="0. " ② -------------------4分
由①②可得
 故函数的解析式为f(x)=x3-x2-x. ----------------8分
故函数的解析式为f(x)=x3-x2-x. ----------------8分 由此得f′(x)=3x2-2x-1.
当f′(x)>0时, x<-
 或x>1。
或x>1。因此在f(x)的单调递增区间为区间(-∞,-
 )和(1,+∞).
)和(1,+∞).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
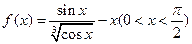 .
.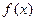 的导数
的导数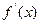 ;
;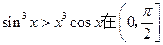 上恒成立;
上恒成立;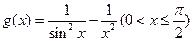 的最大值。
的最大值。 的图象上以N(1,n)为切点的切线的倾斜角为
的图象上以N(1,n)为切点的切线的倾斜角为
 恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
恒成立?如果存在,请求出最小的正整数k;如果不存在,请说明理由;
 ,且函数
,且函数 的图象关于原点对称,其图象在
的图象关于原点对称,其图象在 处的切线方程为
处的切线方程为 (1)求
(1)求 使得函数
使得函数 的定义域和值域均为
的定义域和值域均为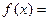
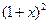 -4
-4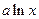 (a∈N﹡).(Ⅰ)若函数
(a∈N﹡).(Ⅰ)若函数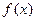 在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程
在(1,+∞)上是增函数,求a的值;(Ⅱ)在(Ⅰ)的条件下,若关于x的方程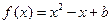 在区间[1,e]上恰有一个实根,求实数b的取值范围.
在区间[1,e]上恰有一个实根,求实数b的取值范围.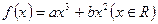 的图像过点P(-1,2),且在点P处的切线恰好与直线
的图像过点P(-1,2),且在点P处的切线恰好与直线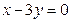 垂直。
垂直。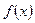 的解析式;
的解析式;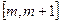 上单调递增,求实数m的取值范围。
上单调递增,求实数m的取值范围。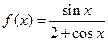 。
。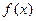 的单调区间;
的单调区间;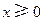 ,都有
,都有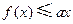 ,求
,求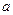 的取值范围。
的取值范围。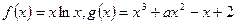
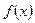 的单调区间;
的单调区间;
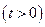 上的最小值;
上的最小值;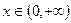 ,
,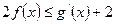 恒成立,求实数
恒成立,求实数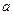 的取值范围.
的取值范围. 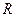 上的奇函数
上的奇函数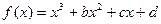 在
在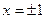 处取得极值.
处取得极值.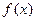 的解析式;
的解析式;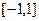 上任意两个自变量的值
上任意两个自变量的值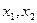 ,都有
,都有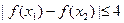 成立;
成立;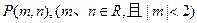 可作曲线
可作曲线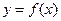 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.