题目内容
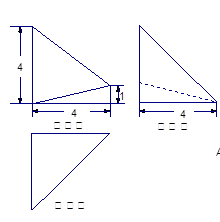
已知四棱锥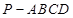 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.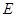 是侧棱
是侧棱 上的动点.
上的动点.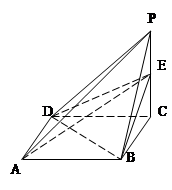

(1)求证: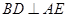 ;
;
(2)若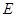 为
为 的中点,求直线
的中点,求直线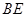 与平面
与平面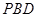 所成角的正弦值;
所成角的正弦值;
(3) 若四点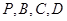 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
(1)参考解析;(2) ;(3)
;(3)
解析试题分析:(1)要证明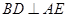 ,要转到线面垂直,通过观察需证明
,要转到线面垂直,通过观察需证明 平面
平面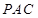 .所以要证明
.所以要证明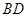 垂直于平面两条相交直线,显然
垂直于平面两条相交直线,显然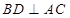 ,
,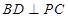 .从而可得结论.
.从而可得结论.
(2)要求直线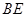 与平面
与平面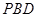 所成角的正弦值,需要找到直线与平面所成的角.通过证明平面
所成角的正弦值,需要找到直线与平面所成的角.通过证明平面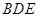
 平面
平面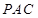 .即可得到点E到平面
.即可得到点E到平面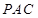 的投影在PO(O是AC与BD的交点)上.这样就可以求出直线与平面所成的角,再通运算即可求出结论.本小题也可已建立空间坐标系来求.
的投影在PO(O是AC与BD的交点)上.这样就可以求出直线与平面所成的角,再通运算即可求出结论.本小题也可已建立空间坐标系来求.
(3)若四点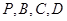 在同一球面上,求该球的体积.依题意可得.只要把图形补齐为一个长方体.外接球的直径就是长方体的对角线长.即可求结论.
在同一球面上,求该球的体积.依题意可得.只要把图形补齐为一个长方体.外接球的直径就是长方体的对角线长.即可求结论.
试题解析:(1)证明:由已知
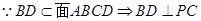 ,
,
又因为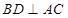 ,
, 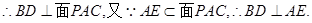
(2)解法一:连AC交BD于点O,连PO,由(1)知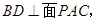
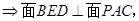
 则
则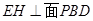 ,
,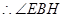 为
为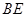 与平面
与平面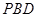 所成的角.
所成的角. 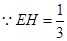 ,
, 则
则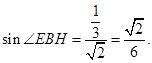
法二:空间直角坐标法,略.
(3)解:以正方形 为底面,
为底面, 为高补成长方体,此时对角线
为高补成长方体,此时对角线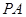 的长为球的直径,
的长为球的直径,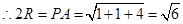 ,
,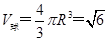
 .
.
考点:1.线线垂直.2.线面所成的角.3.割补思想.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
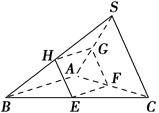
 =2,点G为AC的中点.
=2,点G为AC的中点.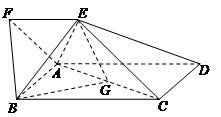
 中,侧面
中,侧面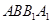 为矩形,
为矩形,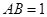 ,
,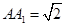 ,
,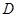 为
为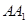 的中点,
的中点,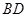 与
与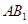 交于点
交于点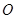 ,
,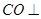 侧面
侧面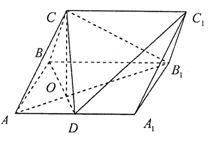
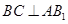 ;
;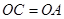 ,求三棱锥
,求三棱锥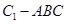 的体积.
的体积.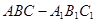 的三视图如图所示,且
的三视图如图所示,且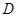 是
是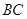 的中点.
的中点.
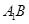 ∥平面
∥平面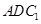 ;
;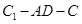 的余弦值;
的余弦值;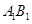 上是否存在点
上是否存在点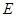 ,使
,使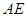 与
与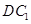 成
成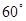 角?若存在,确定
角?若存在,确定
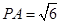 ,
,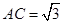 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,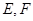 分别是
分别是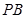 与
与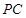 的中点,
的中点,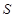 是线段
是线段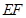 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体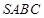 的体积。
的体积。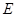 是以
是以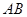 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形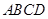 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且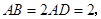
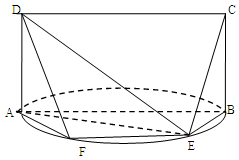
 ;
;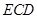 与半圆弧的另一个交点为
与半圆弧的另一个交点为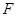 ,
,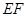 //
//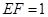 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.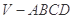 中,底面
中,底面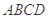 是正方形,侧面
是正方形,侧面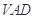 是正三角形,平面
是正三角形,平面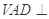 底面
底面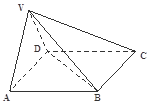
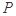 为线段VC的中点,求证:
为线段VC的中点,求证: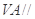 平面
平面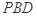 ;
;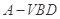 的体积
的体积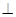 BQ并说明理由.
BQ并说明理由.