题目内容
三棱锥P?ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若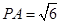 ,
,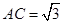 ,PB与底面ABC成60°角,
,PB与底面ABC成60°角,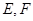 分别是
分别是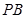 与
与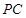 的中点,
的中点,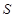 是线段
是线段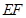 上任意一动点(可与端点重合),求多面体
上任意一动点(可与端点重合),求多面体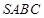 的体积。
的体积。
解析试题分析:(Ⅰ)先利用线面垂直的判定定理证明BC⊥平面PAB,再利用面面垂直的判定定理证明平面PAB⊥平面PBC;(2)由已知条件在在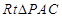 中,计算可得
中,计算可得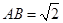 ,可证
,可证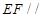 面
面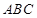 ,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.
,即点S到平面ABC的距离是PA的一半,最后根据棱锥的体积公式计算即可.
试题解析:17、(1)证明:∵PA^面ABC,\PA^BC,
∵AB^BC,且PA∩AB=A,\BC^面PAB
而BCÌ面PBC中,\面PAB^面PBC. 5分
(2)解:PB与底面ABC成60°角,
即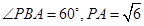 , 6分
, 6分
在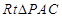 中,
中,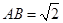 ,又
,又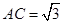 ,
,
在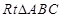 中,
中,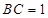 。 8分
。 8分
E、F分别是PB与PC的中点,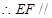 面
面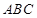 9分
9分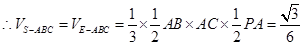 12分
12分
考点:1.平面与平面垂直的判定;2.直线与平面所成的角和二面角.3.棱锥的体积.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
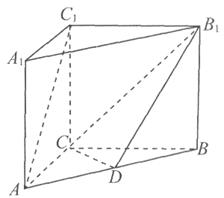
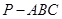 中,
中, ,
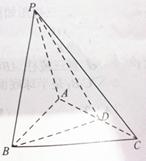
,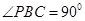 ,D为AC的中点,
,D为AC的中点,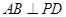 .
.
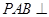 平面
平面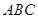 ;
;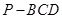 的体积为3,求
的体积为3,求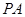 .
.
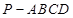 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.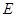 是侧棱
是侧棱 上的动点.
上的动点.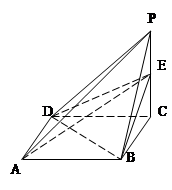

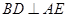 ;
;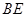 与平面
与平面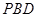 所成角的正弦值;
所成角的正弦值;  在同一球面上,求该球的体积.
在同一球面上,求该球的体积. 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).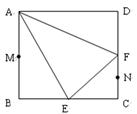
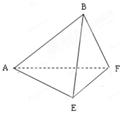
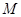 、
、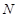 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;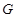 是线段
是线段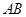 上一点,且
上一点,且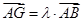 ,问是否存在点
,问是否存在点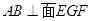 ,若存在,求出
,若存在,求出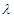 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;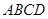 与直角梯形
与直角梯形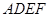 所在平面互相垂直,
所在平面互相垂直,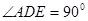 ,
, ,
,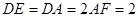 .
.
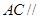 平面
平面 ;
;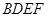 的体积.
的体积. 中,
中,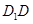
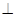 底面
底面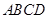 ,
, ,
,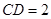 ,
,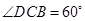 .
.
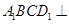 平面
平面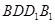 ;
;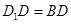 ,求四棱锥
,求四棱锥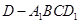 的体积.
的体积.