题目内容
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB= =2,点G为AC的中点.
=2,点G为AC的中点.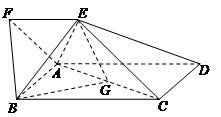
(Ⅰ)求证:EG//平面ABF;
(Ⅱ)求三棱锥B-AEG的体积;
(Ⅲ)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
(I)详见解析;(Ⅱ)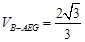 ;(Ⅲ)平面BAE⊥平面DCE.证明见解析.
;(Ⅲ)平面BAE⊥平面DCE.证明见解析.
解析试题分析:(I)取AB中点M,连FM,GM.由题设易得四边形GMFE为平行四边形,从而得EG∥平面ABF;(Ⅱ)显然转化为求三棱锥E-ABG的体积.注意到平面ABCD⊥平面AFED,故作EN⊥AD,垂足为N,则有EN⊥平面ABCD,即EN为三棱锥E-ABG的高.由此即可得其体积;(Ⅲ)为了判断平面BAE、平面DCE是否垂直,首先看看在这两个面中有哪些线是相互垂直的.由平面ABCD⊥平面AFED,四边形ABCD为矩形可得,CD⊥平面AFED,从而 CD⊥AE.另外根据题中所给数据,利用勾股定理可判断ED⊥AE.由此可知,平面BAE⊥平面DCE.
试题解析:(I)证明:取AB中点M,连FM,GM.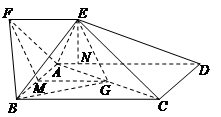
∵G为对角线AC的中点,
∴GM∥AD,且GM=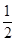 AD,
AD,
又∵FE∥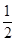 AD,
AD,
∴GM∥FE且GM=FE.
∴四边形GMFE为平行四边形,即EG∥FM.
又∵ 平面ABF,
平面ABF,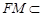 平面ABF,
平面ABF,
∴EG∥平面ABF. 4分
(Ⅱ)解:作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED ,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵在△AEF中,AF=FE,∠AFE=60º,
∴△AEF是正三角形.
∴∠AEF=60º,
由EF//AD知∠EAD=60º,
∴EN=AE?sin60º= .
.
∴三棱锥B-AEG的体积为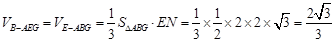 . 8分
. 8分
(Ⅲ)解:平面BAE⊥平面DCE.证明如下:
∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,
∴CD⊥AE.
∵四边形AFED为梯形,FE∥AD,且 ,
,
∴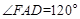 .
.
又在△AED中,EA=2,AD=4,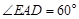 ,
,
由余弦定理,得ED=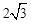 .
.
∴EA2+ED2=AD2,
∴ED⊥AE.
又∵ED∩CD=D,
∴AE⊥平面DCE,
又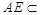 面BAE,
面BAE,
∴平面BAE⊥平面DCE. 12分
考点:1、空间直线与平面的位置关系;2、几何体的体积.

 应用题作业本系列答案
应用题作业本系列答案 的圆锥
的圆锥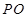 中,已知
中,已知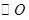 的直径
的直径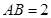 ,
, 是
是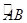 的中点,
的中点,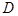 是弦
是弦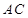 的中点.
的中点.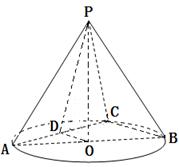
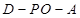 的平面角,并求出它的大小;
的平面角,并求出它的大小;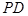 与
与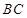 所成的角的正切值.
所成的角的正切值. 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.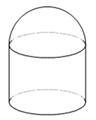
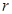 表示出储油灌的容积
表示出储油灌的容积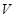 ,并写出
,并写出 与半径
与半径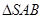 ,
,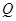 为底面圆周上一点.
为底面圆周上一点.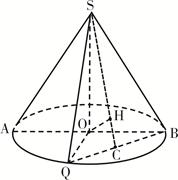
 的中点为
的中点为 ,
,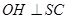 ,
,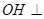 平面
平面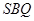 ;
;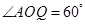 ,
,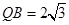 ,求此圆锥的全面积.
,求此圆锥的全面积. ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过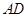 作圆柱的截面交下底面于
作圆柱的截面交下底面于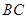 ,四边形ABCD是正方形.
,四边形ABCD是正方形.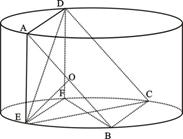
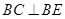 ;
;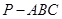 中,
中, ,
,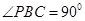 ,D为AC的中点,
,D为AC的中点,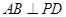 .
.
 平面
平面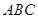 ;
;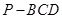 的体积为3,求
的体积为3,求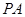 .
.
 ,求三棱锥B1-A1DC的体积.
,求三棱锥B1-A1DC的体积.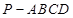 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.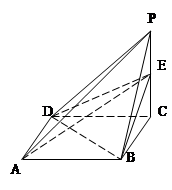

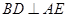 ;
;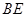 与平面
与平面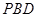 所成角的正弦值;
所成角的正弦值; 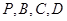 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.