题目内容
如图,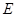 是以
是以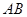 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形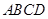 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且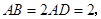
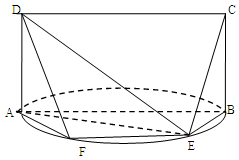
(Ⅰ)求证: ;
;
(Ⅱ)设平面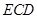 与半圆弧的另一个交点为
与半圆弧的另一个交点为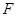 ,
,
①求证: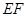 //
//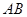 ;
;
②若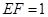 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积.
(Ⅰ) ;(Ⅱ)①
;(Ⅱ)①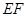 //
//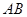 ;②
;②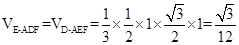 .
.
解析试题分析:(1)证明线线垂直,则可转化为线面垂直,由于圆周角的定义,则知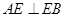 ,由矩形
,由矩形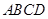 所在的平面垂直于该半圆所在平面,及面面垂直性质定理得
所在的平面垂直于该半圆所在平面,及面面垂直性质定理得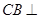 面
面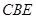 ,则可得平面
,则可得平面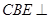 平面
平面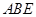
根据垂直的有关性质定理,则可得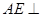 平面
平面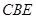 ,故
,故 
(2)①证明线线平行,则可用过平面的一个平行线作于该平面相交的平面,则该直线与交线平行由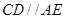 ,得
,得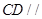 平面
平面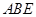 ,又由平面
,又由平面 平面
平面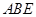 于直线
于直线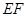 ,则根据线面平行的性质定理得
,则根据线面平行的性质定理得 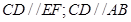 ,由平行的传递性得
,由平行的传递性得 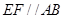 ;②则体积可以用多种方法,有直接求法、割补法、转化法,对于此题可转化后用直接求法,求三棱锥E-ADF先转化
;②则体积可以用多种方法,有直接求法、割补法、转化法,对于此题可转化后用直接求法,求三棱锥E-ADF先转化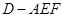 ;根据三棱锥的体积公式,则有
;根据三棱锥的体积公式,则有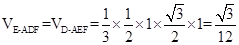
试题解析:
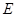 是半圆上异于
是半圆上异于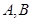 的点,
的点,
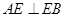 ,又
,又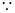 矩形
矩形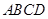 所在的平面垂直于该半圆所在平面
所在的平面垂直于该半圆所在平面 由面面垂直性质定理得
由面面垂直性质定理得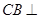 面
面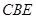 ,
,  平面
平面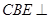 平面
平面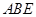

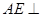 平面
平面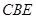 ,故
,故  .
.
(2)① 由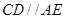 ,得
,得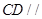 平面
平面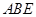 ,又
,又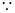 平面
平面 平面
平面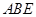 于直线
于直线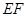 ,
, 根据线面平行的性质定理得
根据线面平行的性质定理得 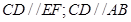 ,故
,故 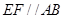 ,②
,②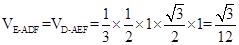 .
.
考点:1.立体几何的平行垂直的证明,2.立体几何体积的求解.

练习册系列答案
相关题目
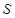 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.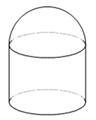
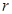 表示出储油灌的容积
表示出储油灌的容积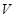 ,并写出
,并写出 与半径
与半径
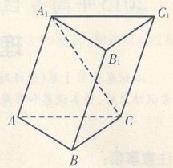
 ,求三棱锥B1-A1DC的体积.
,求三棱锥B1-A1DC的体积. 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.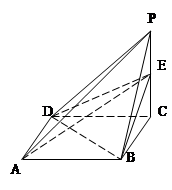

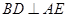 ;
;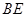 与平面
与平面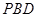 所成角的正弦值;
所成角的正弦值; 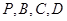 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.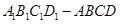 ,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
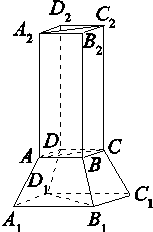
,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱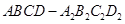 .
.
 平面
平面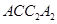 ;
; ,
, ,
,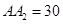 ,
,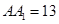 (单位:
(单位: ),每平方厘米的加工处理费为
),每平方厘米的加工处理费为 元,需加工处理费多少元?
元,需加工处理费多少元?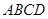 与直角梯形
与直角梯形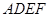 所在平面互相垂直,
所在平面互相垂直,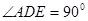 ,
, ,
,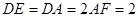 .
.
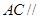 平面
平面 ;
;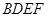 的体积.
的体积.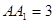 .
.

 B
B