题目内容
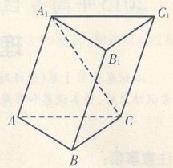
已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ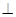 BQ并说明理由.
BQ并说明理由.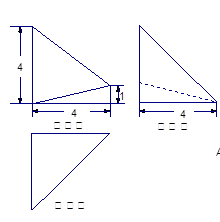
(1)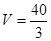 ;(2)
;(2)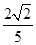 ;(3)存在点Q,使得AQ
;(3)存在点Q,使得AQ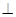 BQ.
BQ.
解析试题分析:(1)由三视图还原几何体为一个锥体,利用锥体体积公式求解;(2)法1:化空间角为平面角,在一个三角形内求值;法2:建立空间直角坐标系求解;(3)法1:假设存在,通过构造面面垂直来实现AQ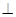 BQ;法2:建立空间直角坐标系,转化为两对应向量数量积为零,求出点Q的坐标.
BQ;法2:建立空间直角坐标系,转化为两对应向量数量积为零,求出点Q的坐标.
试题解析:(1)由该几何体的三视图知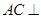 面
面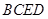 ,且EC="BC=AC=4" ,BD=1,
,且EC="BC=AC=4" ,BD=1,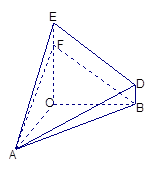
∴
∴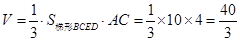 .
.
即该几何体的体积V为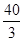 . 3分
. 3分
(2)解法1:过点B作BF//ED交EC于F,连结AF,
则∠FBA或其补角即为异面直线DE与AB所成的角. 5分
在△BAF中,∵AB=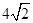 ,BF=AF=
,BF=AF=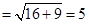 .
.
∴
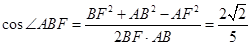 .
.
即异面直线DE与AB所成的角的余弦值为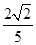 . 7分
. 7分
解法2:以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4)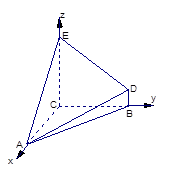
∴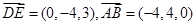 ,∴
,∴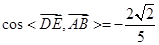
∴异面直线DE与AB所成的角的余弦值为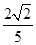 .
.
(3)解法1:在DE上存在点Q,使得AQ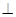 BQ. 8分
BQ. 8分
取BC中点O,过点O作OQ⊥DE于点Q,则点Q满足题设.
连结EO、OD,在Rt△ECO和Rt△OBD中
∵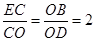
 ∴
∴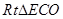 ∽
∽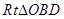
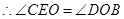
∵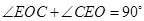 ∴
∴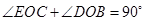
∴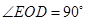 . 11分
. 11分
∵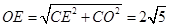 ,
,
∴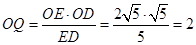
∴以O为圆心、以BC为直径的圆与DE相切.切点为Q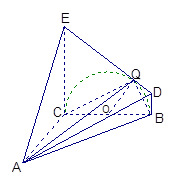
∴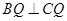
∵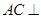 面
面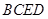 ,
,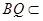 面
面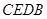 ∴
∴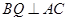 ∴
∴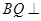 面
面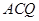 13分
13分
∵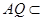 面ACQ
面ACQ
∴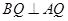 . 14分
. 14分
解法2: 以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
设满足题设的点Q存在,其坐标为(0,m,n),则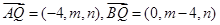
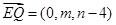 ,
,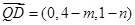
∵AQ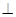 BQ ∴
BQ ∴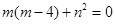 ①
①
∵点Q在ED上,∴存在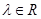
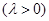 使得
使得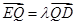
∴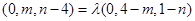
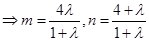 ②
②
②代入①得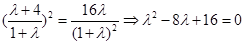 ,解得
,解得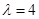
∴满足题设的点Q存在,其坐标为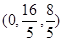 .
.
考点:1.三视图;2.锥体的体积;3.异面直线所成角;4探究性问题证明线线垂直;5.利用空间向量解决几何问题.

 阅读快车系列答案
阅读快车系列答案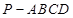 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.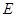 是侧棱
是侧棱 上的动点.
上的动点.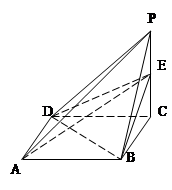

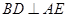 ;
;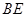 与平面
与平面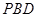 所成角的正弦值;
所成角的正弦值; 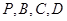 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
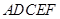 (如图1),
(如图1),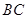 为对称轴,
为对称轴,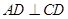 ,
,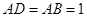 ,
,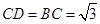 ,将此图形沿
,将此图形沿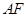 、
、 得到几何体(如图2).
得到几何体(如图2).

 ;
; 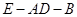 的余弦值.
的余弦值. 是
是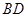 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.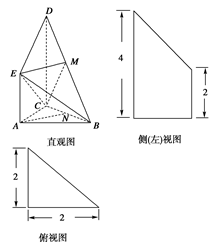
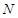 是
是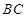 的中点,求证:
的中点,求证: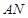 ∥平面
∥平面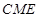 ;
;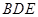 ⊥平面
⊥平面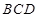 .
. B
B