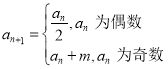题目内容
【题目】已知集合
，元素
成为集合
的特征元素，对于中的元素
与
，定义：
.当
时，若a是集合
中的非特征元素，则
的概率为___.
【答案】
【解析】
根据题意，先得到
，分别确定
中有“
个，
个，
个，
个，
个，
个，
个，
个，
个”所对应的基本事件个数，确定
所包含的基本事件个数，基本事件个数比即为所求概率.
由题意，当
时，
，
则，
又
，
所以取值只能为或
；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
当中有个时，
，此时共包含
个基本事件；
因此的概率为
.
故答案为：.
【题目】当今世界科技迅猛发展，信息日新月异．为增强全民科技意识，提高公众科学素养，某市图书馆开展了以“亲近科技、畅想未来”为主题的系列活动，并对不同年龄借阅者对科技类图书的情况进行了调查．该图书馆从只借阅了一本图书的借阅者中随机抽取100名，数据统计如表：
借阅科技类图书（人） | 借阅非科技类图书（人） | |
年龄不超过50岁 | 20 | 25 |
年龄大于50岁 | 10 | 45 |
（1）是否有99%的把握认为年龄与借阅科技类图书有关？
（2）该图书馆为了鼓励市民借阅科技类图书，规定市民每借阅一本科技类图书奖励积分2分，每借阅一本非科技类图书奖励积分1分，积分累计一定数量可以用积分换购自己喜爱的图书．用表中的样本频率作为概率的估计值．
（i）现有3名借阅者每人借阅一本图书，记此3人增加的积分总和为随机变量ξ，求ξ的分布列和数学期望；
（ii）现从只借阅一本图书的借阅者中选取16人，则借阅科技类图书最有可能的人数是多少？
附：K2
，其中n＝a+b+c+d．
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |