题目内容
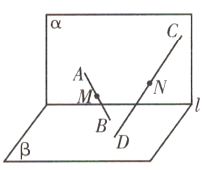
【题目】如图,平面α∩平面β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )
A.若AB![]() CD,则MN
CD,则MN![]() l
l
B.若M,N重合,则AC![]() l
l
C.若AB与CD相交,且AC![]() l,则BD可以与l相交
l,则BD可以与l相交
D.若AB与CD是异面直线,则MN不可能与l平行
【答案】BD
【解析】
由若两两相交的平面有三条交线,交线要么相交于一点,要么互相平行判定![]() 、
、![]() 、
、![]() ;用反证法证明
;用反证法证明![]() .
.
解:若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 四点共面
四点共面![]() ,当
,当![]() 时,
时,
平面![]() 、
、![]() 、
、![]() 两两相交有三条交线,分别为
两两相交有三条交线,分别为![]() 、
、![]() 、
、![]() ,则三条交线交于一点
,则三条交线交于一点![]() ,
,
则![]() 与平面
与平面![]() 交于点
交于点![]() ,
,![]() 与
与![]() 不平行,故
不平行,故![]() 错误;
错误;
若![]() ,
,![]() 两点重合,则
两点重合,则![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 四点共面
四点共面![]() ,
,
平面![]() 、
、![]() 、
、![]() 两两相交有三条交线,分别为
两两相交有三条交线,分别为![]() 、
、![]() 、
、![]() ,
,
由![]() ,得
,得![]() ,故
,故![]() 正确;
正确;
若![]() 与
与![]() 相交,确定平面
相交,确定平面![]() ,平面
,平面![]() 、
、![]() 、
、![]() 两两相交有三条交线,分别为
两两相交有三条交线,分别为![]() 、
、![]() 、
、![]() ,
,
由![]() ,得
,得![]() ,故
,故![]() 错误;
错误;
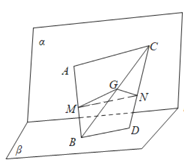
当![]() ,
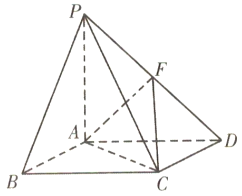
,![]() 是异面直线时,如图,连接
是异面直线时,如图,连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,则
,则![]() ,假设
,假设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,同理可得,平面
,同理可得,平面![]() ,则
,则![]() ,与平面
,与平面![]() 平面
平面![]() 矛盾.
矛盾.
![]() 假设错误,
假设错误,![]() 不可能与
不可能与![]() 平行,故
平行,故![]() 正确.
正确.
故选:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目