题目内容
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
【答案】(1)不具备,理由见解析;(2)![]() 时,
时,![]() 且
且![]() ;
;![]() 时,
时,![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)先假设函数![]() 具有性质
具有性质![]() ,根据题意求出
,根据题意求出![]() ,与
,与![]() 矛盾,即可判断出结果;
矛盾,即可判断出结果;
(2)根据题意,得到![]() ,推出
,推出![]() ,求解,即可得出结果;
,求解,即可得出结果;
(3)根据题意,先得到![]() ,
,![]() ,根据等比数列的定义,以及数学归纳法,分别证明必要性和充分性,即可证明结论成立.
,根据等比数列的定义,以及数学归纳法,分别证明必要性和充分性,即可证明结论成立.
(1)若函数![]() 具有性质
具有性质![]() ;则
;则![]()
即![]() ,
,
所以![]() ,即
,即![]() ,与
,与![]() 矛盾,所以函数
矛盾,所以函数![]() 不具有性质
不具有性质![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,
,
则![]() ,
,
即![]() ,
,
即![]() ,
,
所以![]() ,因此
,因此![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;所以
;所以 ![]() 或
或![]() ;
;
当![]() 时,
时,![]() 且
且![]() ,所以
,所以![]() 且
且![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
(3)因为函数![]() 在
在![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),
),
所以![]() ,
,
又函数![]() 不存在零点,
不存在零点,![]() ,
,
所以![]() ,
,![]() ;
;
下面证明必要性:
若数列![]() 为等比数列,则
为等比数列,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此![]() ,所以
,所以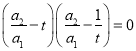 ,即
,即![]() 或
或![]() ;
;
接下来证明充分性:
若![]() ,因为
,因为![]() ,所以
,所以![]() ,因此
,因此![]() ;
;
猜想:![]() ;
;
用数学归纳法证明如下:
①当![]() 时,
时,![]() 显然成立;
显然成立;
②假设![]() 时,
时,![]() 成立,
成立,![]() 成立;
成立;
则当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即![]() 时,
时,![]() 也成立,
也成立,
由①②可得,![]() 恒成立;即数列
恒成立;即数列![]() 为公比是
为公比是![]() 的等比数列;
的等比数列;
同理:![]() 时,数列
时,数列![]() 为公比是
为公比是![]() 的等比数列;
的等比数列;
综上,数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】产量相同的机床一和机床二生产同一种零件,在一个小时内生产出的次品数分别记为![]() ,
,![]() ,它们的分布列分别如下:
,它们的分布列分别如下:
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
(1)哪台机床更好?请说明理由;
(2)记![]() 表示
表示![]() 台机床
台机床![]() 小时内共生产出的次品件数,求
小时内共生产出的次品件数,求![]() 的分布列.
的分布列.