题目内容
【题目】已知![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 满足:
满足: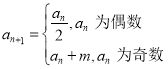 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 为奇数,求证:“
为奇数,求证:“![]() ”的充要条件是“
”的充要条件是“![]() 为奇数”.
为奇数”.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用递推公式直接代入求值.
(2)分类讨论当![]() 为奇数和偶数的情况,再讨论
为奇数和偶数的情况,再讨论![]() 为奇数和偶数的情况,求得
为奇数和偶数的情况,求得![]() 的值.
的值.
(3)先证充分性(易证得),再证必要性,用数学归纳法证明.
解:(1)![]() ,
,![]() ,则前7项为8,4,2,1,3,5,7,故
,则前7项为8,4,2,1,3,5,7,故![]() .
.
(2)由题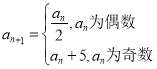 设
设![]() 是整数.
是整数.
①若![]() 为奇数,可设
为奇数,可设![]() ,
,![]() ,则
,则![]() 是偶数,得
是偶数,得![]() ,
,
则![]() ,此时
,此时![]() ,符合题意
,符合题意
②若![]() 为偶数,可设
为偶数,可设![]() ,
,![]() ,则
,则![]() ,
,
当![]() 是偶数时,可设
是偶数时,可设![]() ,得
,得![]()
![]() ,
,![]() ,
,
则![]() ,此时
,此时![]() 不存在.
不存在.
当![]() 是奇数时,可设
是奇数时,可设![]() ,得
,得![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得![]() ,得
,得![]() .
.
综合①②可得,![]() 或
或![]() .
.
(3)充分性:若![]() 为奇数,则
为奇数,则![]() ;
;
必要性:先利用数学归纳法证:![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
①![]() ,
,![]() ,
,![]() 成立;
成立;
②假设![]() 时,
时,![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
③当![]() 时,当
时,当![]() 是偶数,
是偶数,![]() ;当
;当![]() 是奇数,
是奇数,![]() ,此时
,此时![]() 是偶数.
是偶数.
综上,由数学归纳法得![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
从而若![]() 时,必有
时,必有![]() 是偶数.进而若
是偶数.进而若![]() 是偶数,则
是偶数,则![]() 矛盾,故
矛盾,故![]() 只能为奇数.
只能为奇数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目